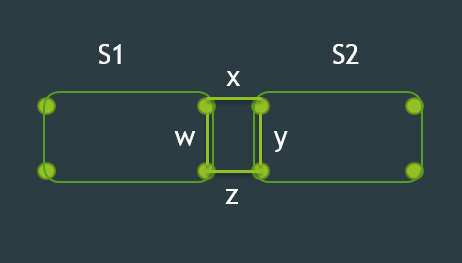CCPC 2014 中程杯紀錄

contents

1. 1. 序
2. 2. 賽前
3. 3. 題目
   1. 3.1. Problem A Non-boring sequences
   2. 3.2. Problem B Traffic Jam
      1. 3.2.1. 觀察
      2. 3.2.2. 推倒
   3. 3.3. Problem C Finding the Prime Implicants of a Boolean Function
   4. 3.4. Problem D Binary String
   5. 3.5. Problem E Digits Count
   6. 3.6. Problem F Math Problem
   7. 3.7. Problem G Better Method
   8. 3.8. Problem H K-Anonymous Sequence
4. 4. 賽後

序

在此先感謝 inker 帶我出門！當然也感謝 彰師大 這次辦的程式競賽。這是一場久違的比賽，同時也是這學期最後一場，原因是因為太久沒參賽，導致往後的桂冠賽也無法參加。

至於討厭比賽的問題，這一篇就不多說了。記得下次繼續支持彰師大資工辦的活動，免得像靜宜大學被玩壞了。 CCPC 官網

賽前

比賽前日進發 inker 豪宅，中間歷經坐錯區間車，到比賽會場前，徒步走了三十分鐘到火車站搭車 … 各種經歷深感出門是件難事。跟我肯定是不幸的，應該多少有點關聯。

上次比賽是很久之前的事情，想到這次還會遭遇國手，還有清華交大的選手，深感害怕。在這情況下，要出門見人什麼的，讓我窩回宿舍吧！

題目

Problem A Non-boring sequences

UVa 1608 - Non-boring sequences

結果題目還是讀錯了，對於任意連續區間，都存在一個獨特的數字。

很容易誤解 connected subsequence 簡單的說就是相鄰兩個元素。
這題由於讀題錯誤，在全場第一個送出的同時拿下的 Wrong Answer。
在假解的情況下，居然通過了測試。

#include<iostream>
#include<stdio.h>
#include<map>
using namespace std;
int t, n, h1,h2;

int main(){
    scanf("%d", &t);
    while(t --){
        scanf("%d", &n);
        map<int, bool> mp;
        int i = 0;
        bool yes = true;
        int pre = -1;
        for(i = 0 ; i < n ; i ++)
        {
            scanf("%d", &h2);
            if(pre == h2){
            
                yes = false;
            }
            pre = h2;
        }
        printf(yes?"non-boring\n":"boring\n");
    }
    return 0;
}

Problem B Traffic Jam

UVa 1417 - Traffic Jam

這題是全場最噁心的題目，但是沒想到有人用 BFS 還是 DFS 在每個詢問就過了。

賽完看到記分板表示非常火。

猜測解法如下，採用線段樹的方式。

觀察

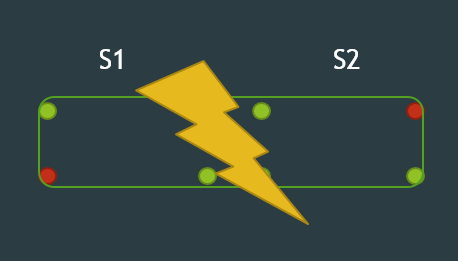
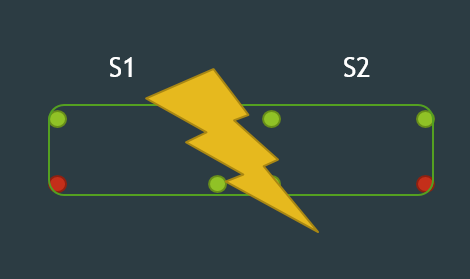
對於任兩點詢問假設這個區間是 [l, r]，不管同側還是異測，當然你也可以假設兩旁還有可以連的。發現對於區間 [l, r] 的點來說，會有左上無法到右下的情況或者左下無法到右上，兩者只有符合一個條件就可以說出 NO。

推倒

因此我們維護區間 [l, r] 的左上到右下、左下到右上的連通性。

對於區間 S 來說，可以切成 S1 和 S2，維護四條資訊，連通性有無 0/1。

• A(左上, 右下) =
  • S1.A & S2.A & (wx || yz)
  • S1.A & S2.D & (z || wxy)
  • S1.C & S2.A & (x || wyz)
  • S1.C & S2.D & (wz || xy)
• B(左下, 右上)
• C(左上, 右上)
• D(左下, 右下)

剩餘 BCD 三條類推，有空的時候再來填滿它，也就是說，之後的開邊跟閉邊都屬於單點更新，因此可以在 O(log n) 時間內完成。對於詢問兩點時，找到 [l, r] 查找 A || B 的結果，由於線段樹會切成數個區間，這個時候要由左而右依序組合即可。

Problem C Finding the Prime Implicants of a Boolean Function

這題就是單純複雜，但是輸入卻不明確。主辦單位有說會忽略空白比對，但是對於 Invaild input format 來說，題目也沒有說清楚輸入格式。

好吧，硬著頭皮做，至少把範例輸入輸出弄了一樣，但是卻砸了。

對了，關於 subset 有個快速地找法。

for(int j = (i-1)&i; j > 0; j--, j &= i) {
    // j 是 i 的 subset
}

這個寫法會在幾題的 UVa 中見到，速度快了 X 倍，不過這題測資沒有強成這樣，也許只是我寫太瘋狂了，想不到更好的解法來完成。最後掛了 Wrong Answer，直接默哀數分鐘。在我心中－她過了。

這題就是窮舉，將每一種組合拆成兩個去合併，而每一種組合(16 bits)如果能合併成一個 product item 則用一個 exist(4 bits) 和 mark(4 bits) 表示，

因此，對於每一個組合拆成 a, b，其中 a.exist == b.exist，同時變數差異只會有一個。

#include <stdio.h>
#include <map>
#include <algorithm>
#include <string.h>
#include <iostream>
#include <sstream>
#include <set>
using namespace std;
//int A[105] = {0, 2, 3, 5,7 ,8, 9, 10, 11, 13, 15}, n = 11;
//int A[105] = {0, 1, 2, 5, 6, 7, 8, 9, 10, 14}, n = 10;
int A[1024], n;
unsigned int result[1<<16] = {};
unsigned int mergeV[1<<16] = {};
struct cmp {
    bool operator()(const int a, const int b) const {
        for(int i = 0; i < 16; i++) {
            int ia, ib;
            ia = (a>>i)&1;
            ib = (b>>i)&1;
            if(ia != ib)
                return ia > ib;
        }
        return a < b;
    }
};
void solv() {
    map<unsigned int, int> combine;
    map<unsigned int, int> combineN;
    for(int i = 0; i < (1<<16); i++) {
        result[i] = mergeV[i] = 0;
    }
    for(int i = 0; i < n; i++) {
        unsigned int mark = 15; // exits
        unsigned int ssss = A[i];
        combine[(ssss<<16)|mark]++;
        combineN[(ssss<<16)|mark] = 1<<A[i];
        result[1<<A[i]] = (ssss<<16)|mark;
        mergeV[1<<A[i]] = 1;
    }
    for(int i = 1; i < (1<<16); i++) {
        if((i&(-i)) == i)
            continue;
        int ok = 0;
        unsigned int V;
        for(int j = 1; j < i; j++) {
            if((i&j) == j) {
                int a, b;
                a = j, b = i^j;
                if(mergeV[a] && mergeV[b]) {
                    unsigned int markA, markB;
                    unsigned int ssssA, ssssB;
                    markA = result[a]&((1<<16)-1);
                    markB = result[b]&((1<<16)-1);
                    ssssA = result[a]>>16;
                    ssssB = result[b]>>16;
                    if(markA == markB) {
                        unsigned int diff = ssssA ^ ssssB;
                        if((diff&(-diff)) == diff) {
                            unsigned int markC = (markA) ^ diff;
                            unsigned int ssssC = min(ssssA, ssssB);
                            ok = 1;
                            combine[result[a]]++;
                            combine[result[b]]++;
                            V = (ssssC<<16)|markC;
                            combineN[(ssssC<<16)|markC] = i;
                            result[i] = (ssssC<<16)|markC;
                            mergeV[i] = 1;
                        }
                    }
                }
            }
        }
        if(ok)
            combine[V]++;
    }
    set< int, cmp > output[20];
    for(map<unsigned int, int>::iterator it = combine.begin();
        it != combine.end(); it++) {
        if(it->second > 1)
            continue;
        /*printf("merge %d: count %d \n", it->first, it->second);*/
        
        unsigned int markA;
        unsigned int ssssA;
        markA = it->first&((1<<16)-1);
        ssssA = it->first>>16;
        int cc = combineN[it->first];
        /*for(int i = 0; i < 4; i++) {
            printf("%d ", (markA>>i)&1);
        }
        puts("  e ");
        for(int i = 0; i < 4; i++) {
            printf("%d ", (ssssA>>i)&1);
        }
        puts("");
        for(int i = 0; i < 16; i++) {
            if((cc>>i)&1)
                printf("%d ", i);
        }
        puts("");*/
        int osize = 0;
        for(int i = 0; i < 16; i++) {
            if((cc>>i)&1)
                osize++;
        }
        output[osize].insert(cc);
    }
    int f = 0;
    for(int k = 16; k >= 0; k--)
        for(set< int >::iterator it = output[k].begin();
            it != output[k].end(); it++) {
            int cc = (*it);
            if(f)	printf(",");
            f = 1;
            putchar('(');
            int f2 = 0;
            for(int i = 0; i < 16; i++) {
                if((cc>>i)&1) {
                    if(f2)	printf(", ");
                    f2 = 1;
                    printf("%d", i);
                }
            }
            putchar(')');
        }
    puts("");
}
int main() {
    char in[1024];
    while(gets(in)) {
        int error = 0;
        for(int i = 0; in[i]; i++) {
            if(in[i] == ')')
                in[i] = ' ';
            else if(in[i] == '(')
                in[i] = ' ';
            else if(in[i] == ',')
                in[i] = ' ';
            else if(in[i] <= '9' && in[i] >= '0')
                continue;
            else
                error = 1;
        }
        stringstream sin(in);
        int number;
        n = 0;
        while(sin >> number) {
            A[n++] = number;
        }
        if(n >= 1024)
            while(1);
        sort(A, A+n);
        int ok = 1;
        for(int i = 0; i < n; i++)
            if(A[i] < 0 || A[i] > 15)
                ok = 0;
        if(ok == 0 || error) {
            printf("Invalid input format");
            continue;
        }/*
        printf("%d\n", n);
        for(int i = 0; i < n; i++)
            printf("%d\n", A[i]);*/
        solv();
    }
    return 0;
}
/*
(0,2,5,8,10)
(0,2,3,5,7,8,9,10,11,13,15)
(0,1,2,5,6,7,8,9,10,14)
(0,1,2,4,5,6,8,9,12,13,14)
(0,1,2,5,6,7,8,9,10,16)
*/

Problem D Binary String

雖然詢問每個參數最大上限後，發現在 m = 100 的情況下，窮舉有點刺激，但是題目卻是要求輸出每一種組合，所以想必組合也不會太多，所以直接亂來吧！

至於以下代碼的正確性就交給神吧，反正都是亂做過的。

#include <stdio.h>
#include <algorithm>
#include <string.h>
using namespace std;

int n, m, s_ones;

char s[105], ret[105];
int slen = 0;
void dfs(int idx, int ones, int has) {
    if(ones > m)
        return;
    if(has == 0 && idx - slen >= 0) {
        int ok = 1;
        for(int i = idx - slen, j = 0; j < slen; j++, i++) {
            ok &= ret[i] == s[j];
        }
        if(ok)
            has = 1;
    }
    if(idx == n) {
        if(ones != m || !has)
            return;
        ret[n] = '\0';
        puts(ret);
        return;
    }
    ret[idx] = '0';
    dfs(idx+1, ones, has);
    ret[idx] = '1';
    dfs(idx+1, ones+1, has);
}
int main() {
    while(scanf("%d %d %s", &n, &m, s) == 3) {
        s_ones = 0;
        for(int i = 0; s[i]; i++)
            s_ones += s[i] == '1';
        slen = strlen(s);
        dfs(0, 0, 0);
    }
    return 0;
}

Problem E Digits Count

這題在 UVa 見過，但是要在比賽中打出來，卻卡死兩個很久沒用腦的人，直到鎖版 (最後一個小時) 才湊出來。

#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;

int mpow(int n, int m) {
    int ret = 1;
    for(int i = 1; i <= m; i++)
        ret *= n;
    return ret;
}
void calc(int n, int cnt[]) {
    if(n <= 0)
        return;
    //printf("%d\n", n);
    char buf[105];
    sprintf(buf, "%d", n);
    int len = strlen(buf);
    int prev = 0, suffix;
    calc(mpow(10, len-1)-1, cnt);
    //for(int i = 0; i < 10; i++)
    //	cnt[i] = 0;
    int prev10 = 1;
    for(int i = 0; i < len; i++) {
        int d = buf[i] - '0';
        sscanf(buf+i+1, "%d", &suffix);
        
        if(i != len-1)
            cnt[d] += suffix + 1;
        else
            cnt[d]++;
        if(i != 0)
            cnt[d] += (prev - prev10/10) * mpow(10, len-i-1);
    //	pritnf("%d \n", );
    //	puts("");
        for(int j = i == 0; j < 10; j++) {
            if(j == d)	continue;
            if(j < d) {
                if(prev > 0) {
                    cnt[j] += (prev - prev10/10 + 1) * mpow(10, len-i-1);
                    //printf("%d %d\n", j, (prev - prev10/10 + 1) * mpow(10, len-i-2));
                } else {
                    cnt[j] += mpow(10, len-i-1);
                    //printf("%d %d\n", j, mpow(10, len-i-1));
                }
            } else {
                if(prev > 0 && prev - prev10/10 > 0) {
                    cnt[j] += (prev - prev10/10) * mpow(10, len-i-1);
                    //printf("%d %d\n", j, (prev - prev10/10 + 1) * mpow(10, len-i-2));
                }
            }
        }
        prev10 *= 10;
        prev = prev * 10 + d;
    }
    /*for(int i = 0; i < 10; i++)
		printf("%d ", cnt[i]);
	puts("");*/
}
void brute(int n) {
    int cnt[10] = {};
    char buf[105];
    for(int i = 1; i <= n; i++) {
        sprintf(buf, "%d", i);
        for(int j = 0; buf[j]; j++)
            cnt[buf[j]-'0']++;
    }
    for(int i = 0; i < 10; i++)
        printf("%d ", cnt[i]);
    puts("");
}
int main() {
    
    
    int l, r;
    /*while(scanf("%d", &l) == 1) {
		brute(l);
		int cnt[10] = {};
		calc(l, cnt);
		for(int i = 0; i < 10; i++)
			printf("%d ", cnt[i]);
		puts("");
	}*/
    while(scanf("%d %d", &l, &r) == 2) {
        if(l == 0 && r == 0)
            break;
        int A[10] = {}, B[10] = {};
        calc(l-1, A);
        calc(r, B);
        for(int i = 0; i < 10; i++)
            printf("%d%c", B[i] - A[i], i ==  9 ? '\n' : ' ');
        
    }
    return 0;
}

Problem F Math Problem

大數二分開 n 方，根據別組的討論，才發現數字其實還挺小的，用 double 型態做 log 運算即可。

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.math.BigInteger;
import java.util.*;
public class A {
    public static void main(String args[]) throws Exception { // µ{¦¡¶i¤JÂI
        Scanner cin = new Scanner(System.in);
        while(cin.hasNext()) {
            int n = cin.nextInt();
            String p = cin.next();
            if(n == 1) {
                System.out.println(p);
                continue;
            }
            BigInteger bigp = new BigInteger(p);
            BigInteger l = BigInteger.ZERO;
            BigInteger r = new BigInteger(p);
            BigInteger m = l, mid, mmid;
            while(l.compareTo(r) <= 0) {
                mid = l.add(r).shiftRight(1);
                mmid = mid.pow(n);
                if(mmid.compareTo(bigp) <= 0) {
                    l = mid.add(BigInteger.ONE);
                    m = mid;
                } else
                    r = mid.subtract(BigInteger.ONE);
            }
            System.out.println(m);
        }
    }
}

Problem G Better Method

聽說是曾經的萬年測試題，這次難得變成主角，肯定是想要每組至少都能帶一題回去。跟 ICPC 一樣的設計方式呢。

#include <stdio.h>
#include <algorithm>
using namespace std;
int f(int n) {
    int ret = n;
    while(n >= 3) {
        ret += n/3;
        n = n%3 + n/3;
    }
    return ret;
}
int main() {
    int n;
    while(scanf("%d", &n) == 1) {
        int v = max(f(n), f(n+1)-1);
        printf("%d\n", v);
    }
    return 0;
}

Problem H K-Anonymous Sequence

本次第二難的題目，但比賽時也是用假解過的，實質為單調對列，可以在 O(n) 時間內完成。至於假解的方式就不方便提供。

賽後

UVa 2000+ 才到這了，腦部硬體的差距就是如此地遙遠，即使捨去其他應用軟體，仍然趕不上嗎？

Rank	Name	Solved	Time	    A    	    B    	    C    	    D    	    E    	    F    	    G    	    H    	Total att/solv
1	team22	6	608	1/11	2/58	0/--	3/141	1/221	1/50	1/67	5/--	14/6
2	team2	6	844	2/32	7/--	14/--	1/108	1/244	1/19	1/11	8/270	35/6
3	team4	5	530	1/7	1/281	26/--	1/217	1/--	1/9	1/16	0/--	32/5
4	team17	5	698	2/13	1/105	1/--	4/296	0/--	1/167	1/37	3/--	13/5
5	team1	5	958	3/286	0/--	4/240	4/--	1/178	1/69	1/85	0/--	14/5
6	team12	4	177	1/11	0/--	3/--	0/--	1/138	1/17	1/11	0/--	7/4
7	team3	4	359	1/108	0/--	5/--	0/--	1/188	1/35	1/28	0/--	9/4
8	team23	4	776	1/12	7/278	0/--	0/--	0/--	1/57	5/229	0/--	14/4
9	team20	4	815	8/131	4/159	0/--	0/--	0/--	1/164	1/161	0/--	14/4

名次	學校學系	隊名
第一名	國立成功大學資訊工程學系	ItsNotCode
第二名	國立中央大學資訊工程學系	Morri$
第三名	國立清華大學資訊工程學系	ISeaTeL
佳作	國立成功大學資訊工程學系	Insert
佳作	國立臺北大學資訊工程學系	Forward Thinking
佳作	國立清華大學資訊工程學系	JustInTime