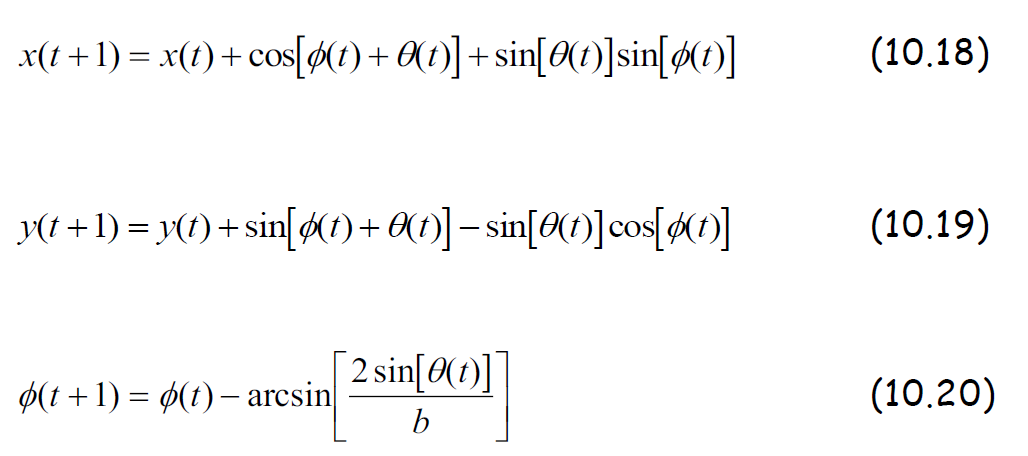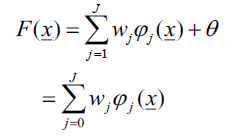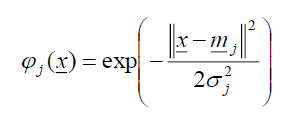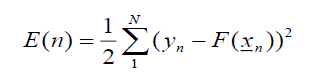學校課程/計算型智慧

計算型智慧 程式作業

contents

  1. 1. Computational Intelligence 計算型智慧
    1. 1.1. Lv. 0 模擬器
    2. 1.2. Lv. 1 模糊系統
      1. 1.2.1. 函數實驗
      2. 1.2.2. 函數設計
    3. 1.3. Lv 2. GA
      1. 1.3.1. 實驗方法
      2. 1.3.2. 實驗結果
      3. 1.3.3. 實驗分析
    4. 1.4. Lv. 3 PSO
      1. 1.4.1. 實驗分析
  2. 2. Github Download

Computational Intelligence 計算型智慧

本課程將會有三階段程式，將三個算法依序加入程式中，為了要實作這些算法，必須先作出模擬器。

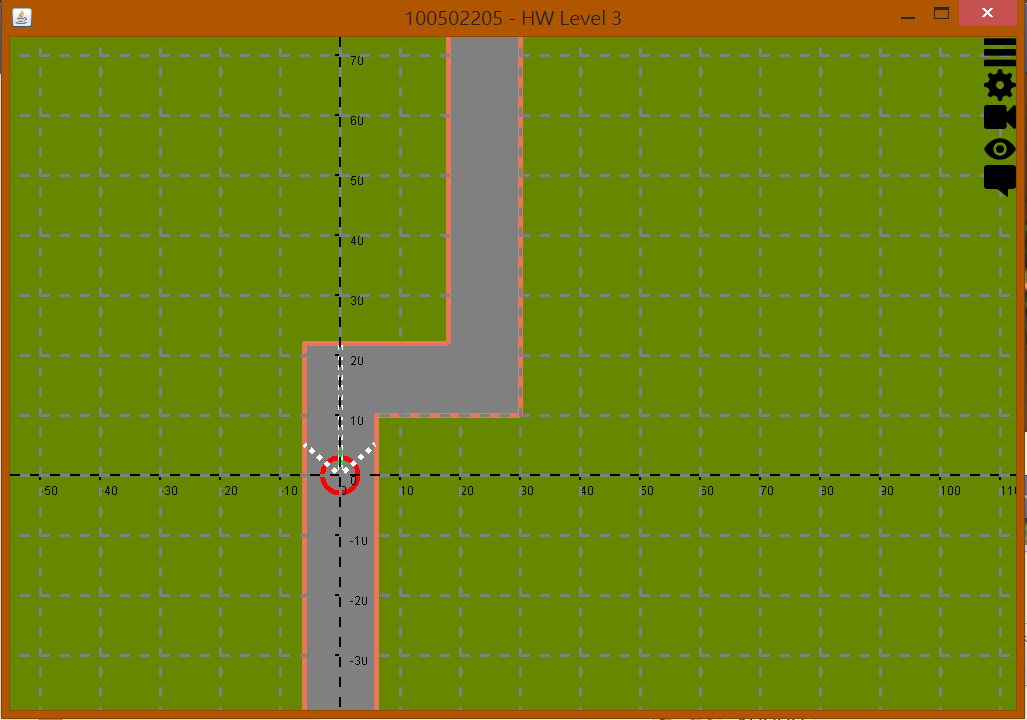
Lv. 0 模擬器

在一個 2D 平面中，以一個圓形當作車子，道路為線段的方式進行描述。為了在隨後的擴充，將地圖內容物分成可行區域多邊形和障礙物多邊形。

  • 要支持車子下一秒的擺角，並且按下推動鍵會根據方程式進行移動。
  • 可以將車子兩側的感測器進行角度調整，並且可以根據感測器角度進行距離計算。
  • 並且在呈現 2D 平面時，附加顯示座標軸的比例。

完成圖

由於私心，有一些額外產物。

  • 完成可以自動置中的設定
  • 提供地圖縮放和讀取操作
  • 製作地圖產生器 (other project)
  • 模擬器的彈木遊戲番外篇 (other project)
  • 提供運行欄位的縮起

Lv. 1 模糊系統

車子運行公式

運行公式

其中 Φ(t) 是模型車與水平軸的角度，b 是模型車的長度，x 與 y 是模型車的座標位置， Θ(t) 是模型車方向盤所打的角度，我們對模擬的輸入輸出變數限制如下：

-40 deg <= Θ(t) <= 40 deg

寫一個程式使用模糊系統、理論模擬車子行徑，並且想辦法最佳化。

  • 考慮擴充性，以後車子的運行公式可能會替換，因此建造一個 Engine class。
  • 模糊系統的幾個特性拆分成數個 method，並且使用不同的數學計算採用繼承關係。
  • 最困難得地方在於計算函數交集，採用離散取點是最後的手段

函數實驗

  1. 經過實驗，三個感測器分別坐落於前方 (90度)、左右各偏轉 50 度左右的夾角比左右 90 度更好。用以應付多變的轉角彎度，防止模稜兩可的擺動。
  2. 不管哪裡種去模糊化系統，由於題目限制擺角於 [-40, 40] 度之間，因此很容易在加權平均、質心、離散化而導致邊界擺角的機率甚低，當越多函數則稀釋程度越高。因此函數定義可以超過限制擺角，只需要在去模糊化時，約束至條件內即可。
  3. 設計函數時，要討論向其中一個方向偏轉，也就是不能設計過於對稱的圖形，否則將會在死胡同裡打轉。

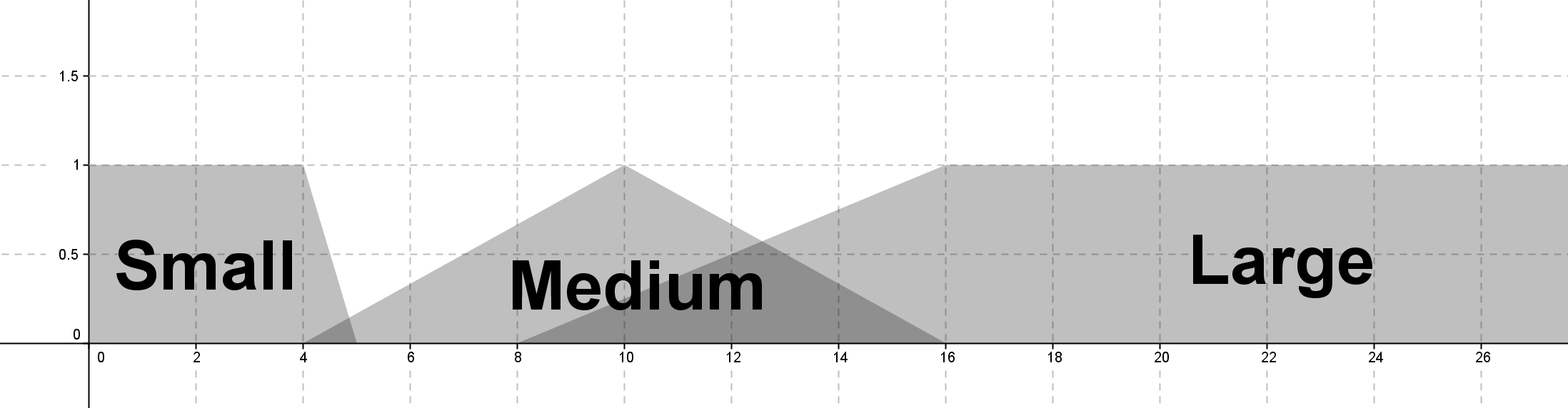
函數設計

d1 為前方感測器，d2 為右方感測器，d3 為左方感測器。

  1. d1 歸屬函數為
    d1 歸屬函數
    d2, d3 歸屬函數為
    d2, d3 歸屬函數
  2. 函數式加權平均
    If d3 large, θ = 55
If d2 large, θ = -55
If d2 medium, θ = -40
If d3 medium, θ = 40
If d1 large and d2 small, θ = -30
If d1 large and d3 small, θ = 30
If d1 small, θ = -60
    規則如上述七條，以最簡單的常數關係。測試結果還算不錯。
    if condition, then statement，statement 中的變數不存在於 condition 去做調整，後來發現由於太複雜去討論而一直失敗。

  3. 重心法、最大平均法、修正型最大平均法、中心平均法
    為了方便計算連續函數，採用離散取點，間隔 0.1 抓取 [-60, 60] 之間的點座標。對於以下四種方法討論於簡單彎道的過程記錄：
    If d3 large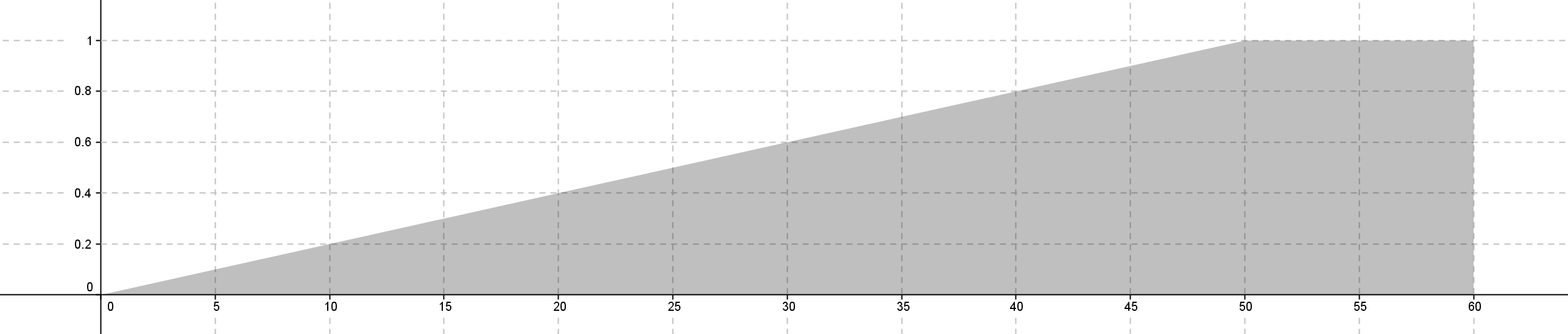
    If d3 large
    If d2 large
    If d2 large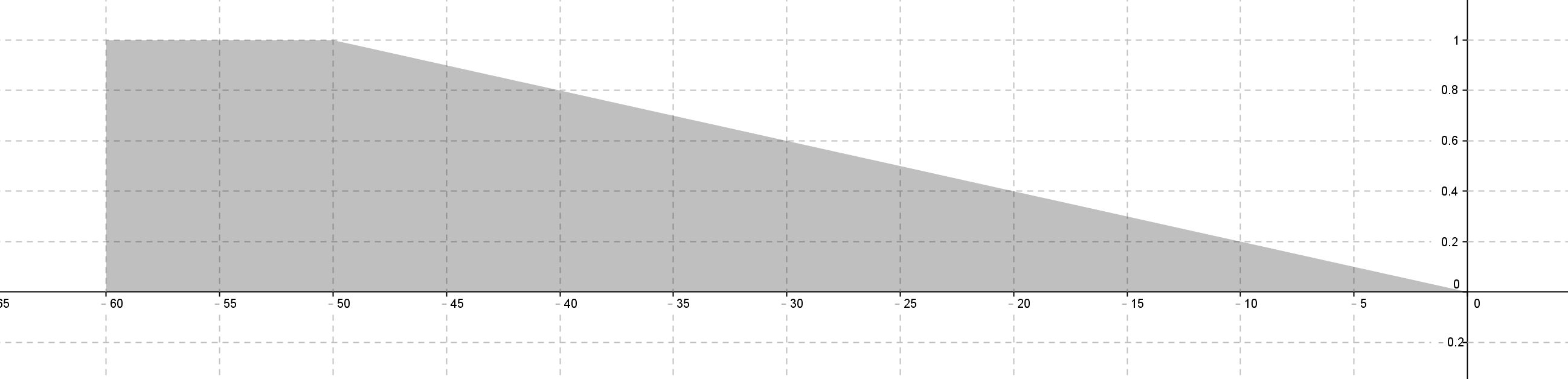
    If d2 medium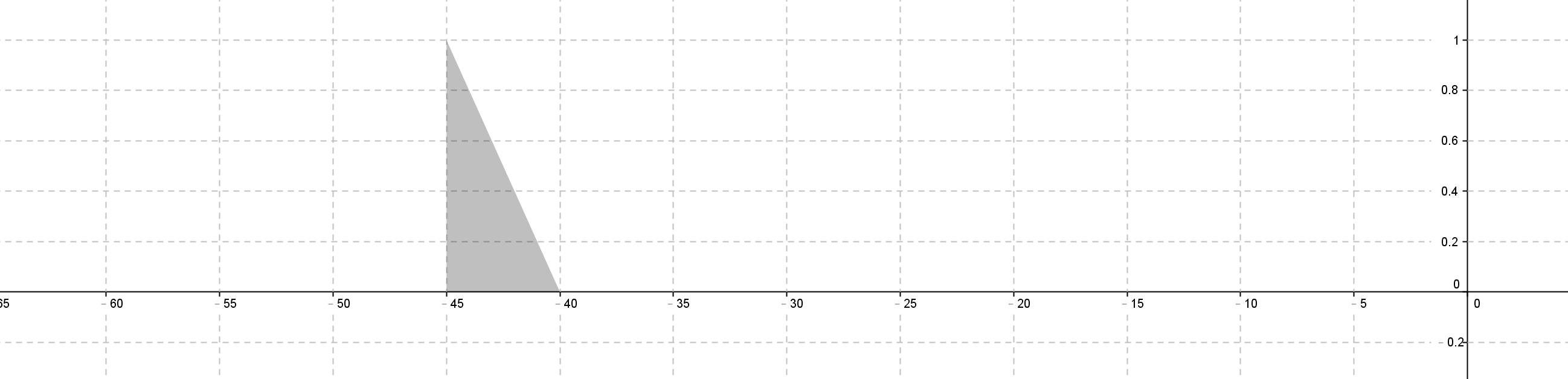
    If d2 medium
    If d3 medium
    If d3 medium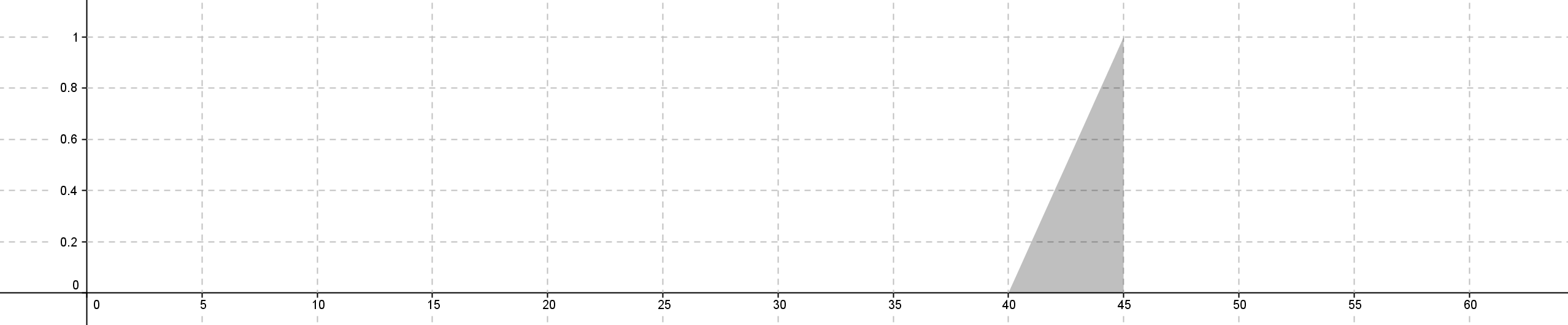
    If d1 large and d2 small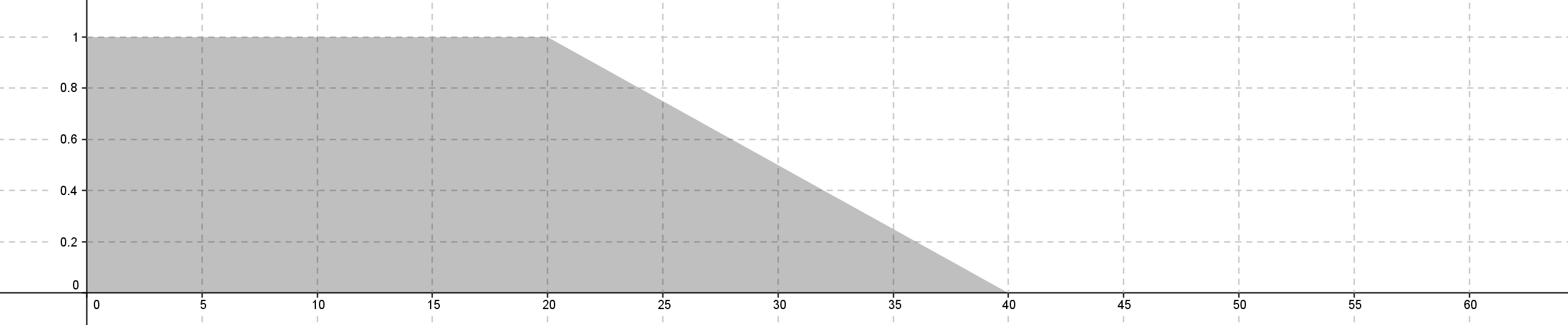
    If d1 large and d2 small
    If d1 large and d3 small
    If d1 large and d3 small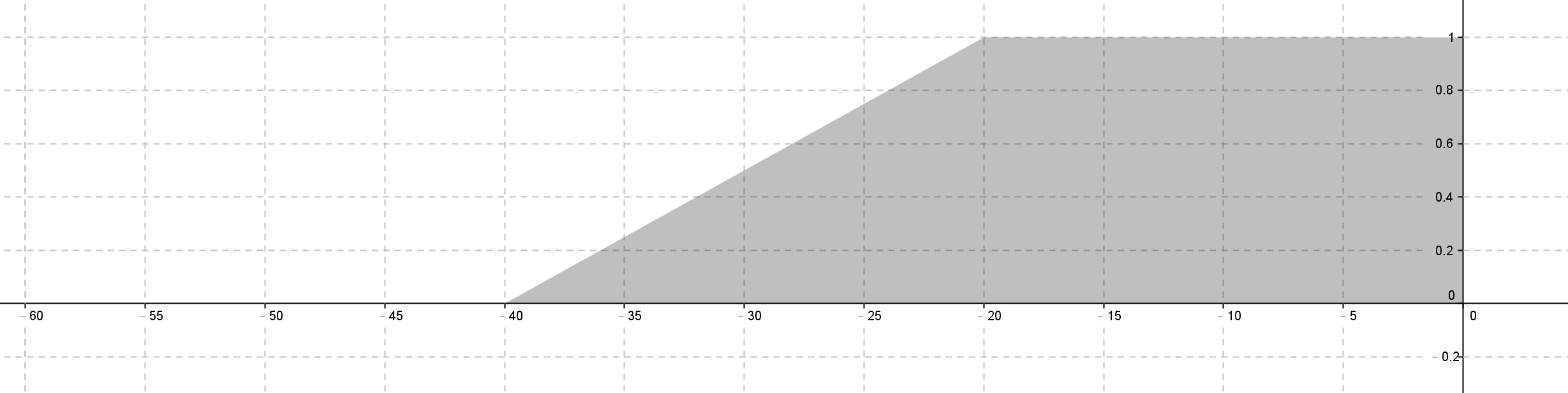
    If d1 small, θ = -60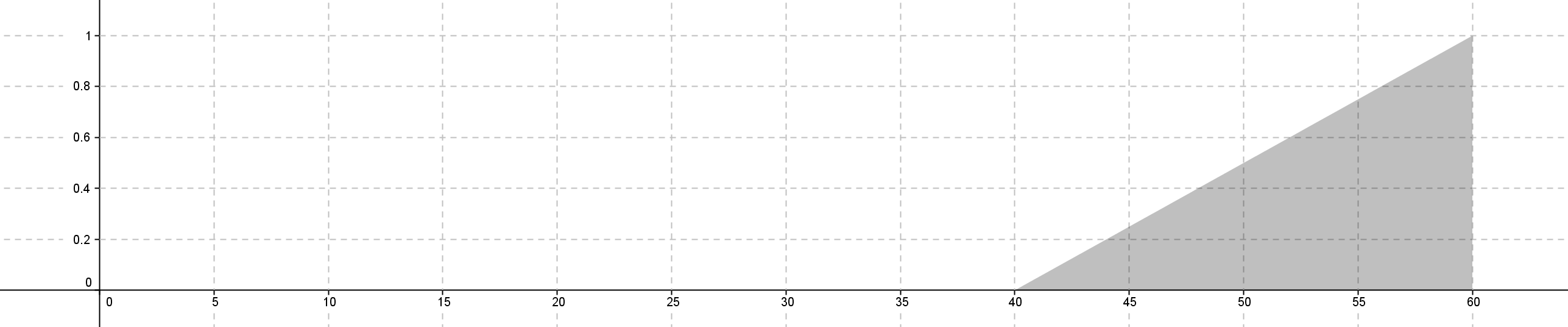
    If d1 small

    • 重心法
      當中表現最為穩健，而且路徑平滑。
    • 最大平均法
      由於定義的函數較為簡單，而且大多都是以梯形的方式存在，雖然能在機率高的情況下走完全程，路徑中會呈現左右擺盪情況。並且大多都已極值的方式出現。
    • 修正型最大平均法
      情況會稍微好一些，但是對於並沒有向重心法一樣的圓滑曲線，仍是因為原先的函數設計所惹的問題。

    對於某一種方法而去定義相關的函數進行測較好，而在最大平均法的部分，必須使用較具有變化性的曲線，否則很容易在極值狀況下擺動。

Lv 2. GA

RBF

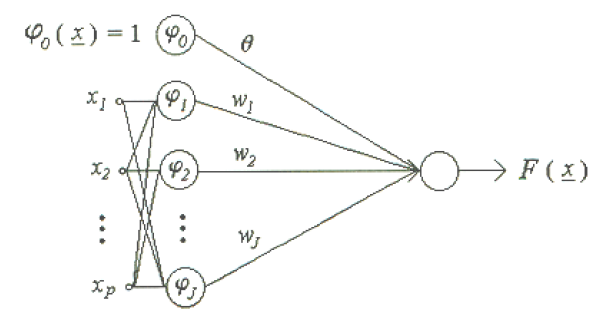
「放射狀基底函數網路 RBF」，基本上，其網路架構如圖1所示，為兩層的網路；假設輸入維度是p ，以及隱藏層類神經元的數目是J ，那麼網路的輸入可以表示成：

其中選用高斯型基底函數：

其中 x = (x1,x2,…,xp) 、mj = (mj1,mj2,…,mjp) 、|| || 代表向量絕對值
適應函數為：

請用實數型基因演算法，找出wj , mj , σj，在不同的數字J下，最好的基因向量 (例如J為9、輸入x為3維向量，則表示基因向量是1+9+3x9+9=46維度的向量，請注意這裡不是指族群數；又例如J為7、輸入x為3維向量，則表示基因向量是1+7+3x7+7=36維度的向量)下，評估函數E(式1)為越小越好。其中基因向量維度公式為 1+J + pJ+J = (p+2)J+1維向量( ,w1 , w2 ,.., wJ , m11, m12,.., m1p, m21, m22,.., m2p,.., mJ1, mJ2,…, mJp, σ1, σ2, …, σJ)。

參數說明 :

  • N 作業1產生的N筆成功到達目的訓練資料(換不同起始點)
  • yn 表示訓練資料的方向盤期望輸出值 P.s.如果配合wj值的範圍為0~1之間，在此則必須把yn由-40~+40度正規化到 0~1之間；如果不想正規化 就必須把 wj的值範圍調整到 -40~40之間 範圍為0~1之間
  • Wj 範圍為 0~1 (或是-40~40)之間 P.s.此需配合訓練集的yn跟F(n)值範圍，所以皆需正規化到0~1之間；若不正規化，wj的值範圍為 -40~40之間
  • mj 範圍跟X範圍一樣，如以提供的範例檔則為 0~30
  • σj 範圍為0~10之間；也可以設定更大的範圍做探討。

實作概要 ：
把參數編碼成 DNA，使用 GA 算法改變 DNA，然後用之前的模糊系統的結果，讓 RBF 接近之前定義的模糊系統。需要拿模糊系統的一些測資當作訓練資料，收集之後餵給 GA 做訓練。

實驗方法

  1. 核心代碼，對於每次迭代，著手適應、選擇、交配、突變。
  2. 細部 “交配” 代碼，採用實數型的分離和聚集兩種情況。
  3. 細部 “突變” 代碼，採用微量雜訊，唯一不同的地方在於，這個微量雜訊會根據當前數值的比例有關，為了避免大數字對於微量雜訊的干擾不夠強烈。

實驗結果

  1. 運行結果 J = 3, p = 3
    ( ,w1 , w2 ,.., wJ , m11, m12,.., m1p, m21, m22,.., m2p,.., mJ1, mJ2,…, mJp, σ1, σ2, …, σJ) = (0.163568 0.851471 1.594151 1.379580 13.092824 0.000505 12.611789 30.000000 0.000368 18.715240 0.000850 2.708967 30.000000 6.307677 7.584529 10.000000)
  2. 訓練數據為 “map2” 走一圈的訓練資訊，約為 500 筆。因為 “map0” (即本次作業給的地圖) 的複雜度不夠以至於無法充分表達原本設計的模糊系統。也就是根據當初模糊系統設計，收集的數據的多樣性和連續性不足。

實驗分析

根據 RBF 的神經元，這裡可以越少越好，在程式中，神經元個數(J) 設置 3 個。運行時採用輪盤式選擇，讓適應能力好的，具有較高的機會繁殖，採用一個隨機變數去挑選。而在基因方面使用實數型基因的形式。

  1. 運行時，突變機率和突變比例相當重要，由於相同適應能力好的物種量很多，只保留其中一部分即可，因此可以將突變機率0.5 左右，太低則會造成進化速度太慢，太高則容易失去原本適應好的物種，導致整體適應度的震盪。
  2. 另外設置突變的比例，也就是該段實數值上下調整的比例。
    g.getDNA()[i] = g.getDNA()[i] + ratio * Math.random() * g.getDNA()[i];
    藉由上述的式子，將 ratio 設置成一個調變比例，來製造爆炸效應的規模。而在運行時，突變效果還能接受。
  3. 原本運行時，只將 DNA 片段的值任意放置，並且約束在不會超出函數的定義域，在收斂速度上有明顯加速。但為了符合作業需求，將每個參數約束在指定範圍內，在收斂速度慢了一截，在預期結果並沒有很好。
  4. 在不同地圖收集的預期資訊，會針對不同車子感測器的角度有所差異，因此不能拿不同型的感測數據，訓練出來的 RBF 不能給另外一台車子來使用，除非使用的感測器角度相當接近。
  5. 對於死路的轉彎，在神經元個數(J) 等於 2 的時候，運行結果較為不佳，但是在本次作業中，並不會有這種數據的出現，也不用考慮這種情況。但是當神經元個數少時，GA 算法的運行速度是相當快的。

Lv. 3 PSO

請利用Particle swarm optimization替換掉 GA 部分。

  • AgentNum(粒子數)
  • IterationNum(疊代數),
  • MaxV(最大速度),
  • MaxX(最大值範圍),
  • Weights(兩個權重),
  • Convergent_Error(停止條件)
  • 並畫出 fitness function 曲線變化 (每一次疊代的最佳fitness值)，最後訓練完成的F(x)當作規則 請跑出車子軌跡。

實驗分析

一開始參數為

1
2
3
4
5
6
public int sandSize = 512;
public double maxVelocity = 0.5;
public double maxXposition = 0.5;
public double weightOfCognition = 0.5;
public double weightOfSocial = 0.5;
public double nearRatio = 0.5;

PSO 1

PSO 2

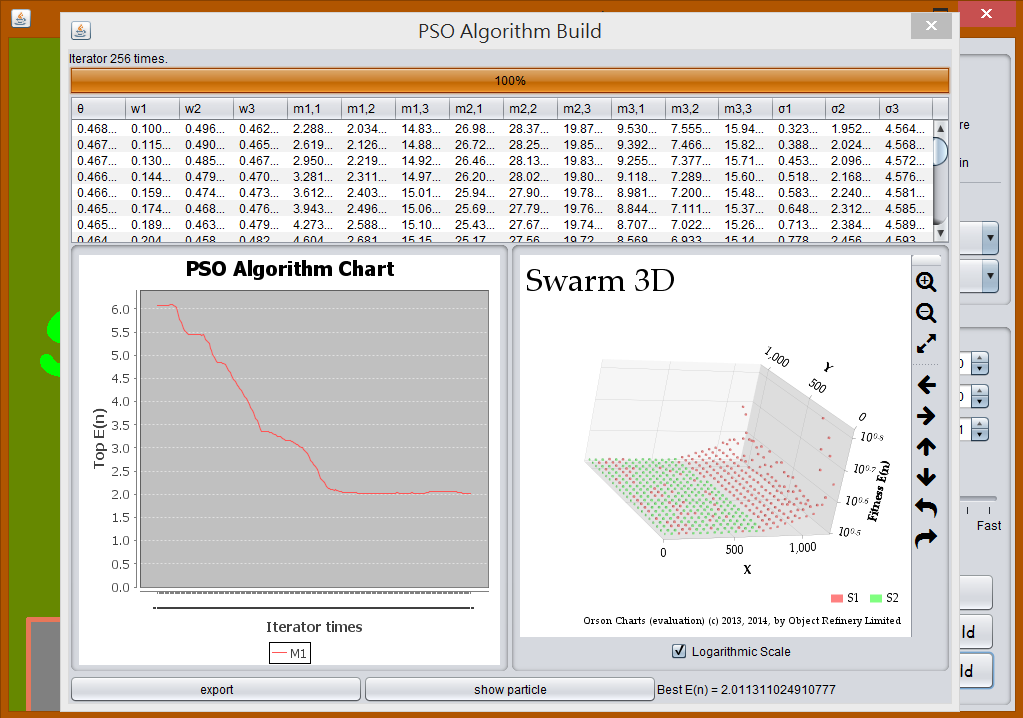
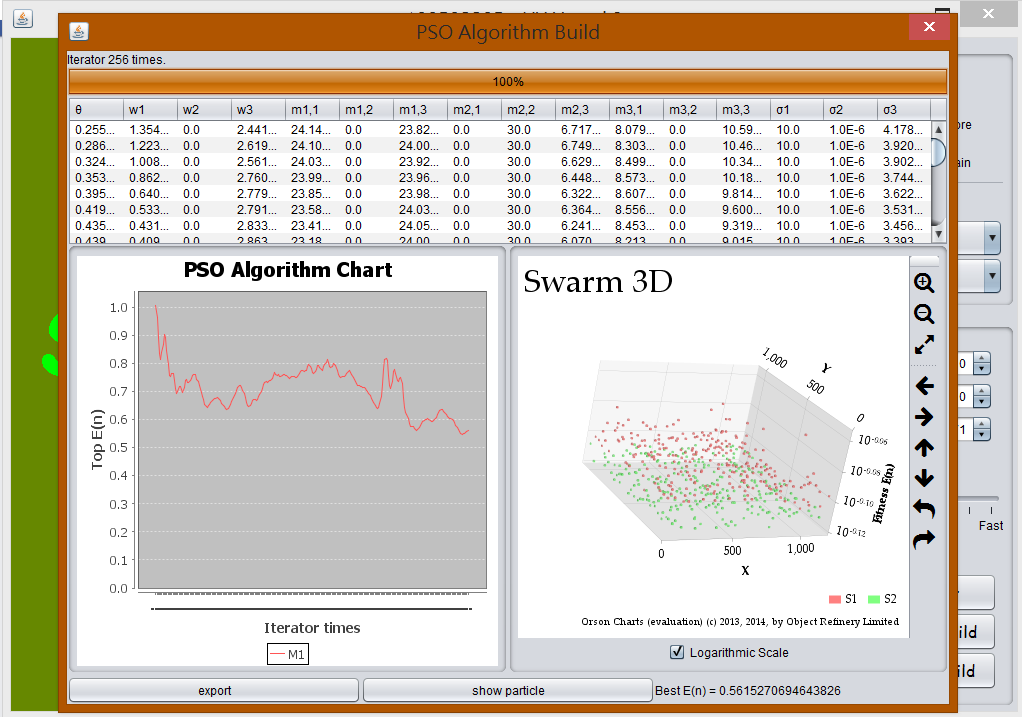
  • 基本上 maxXposition 沒有用到，調整其他比例可以發現端倪。

  • 從圖 PSO 2 中可以發現到，PSO 與 GA 最大的不同在於，如果 GA 調用部分突變的情況下，很高的機率會發現適應曲線是嚴格遞減的，但是在 PSO 由於會飛來飛去，有可能會來回震盪。

  • 當所有粒子逼近最佳解時，仍會以原本的速度繼續飛行，而原本屬於最佳位置的點也會開始模仿其他粒子飛行，如此一來就會造成震盪。

PSO 3

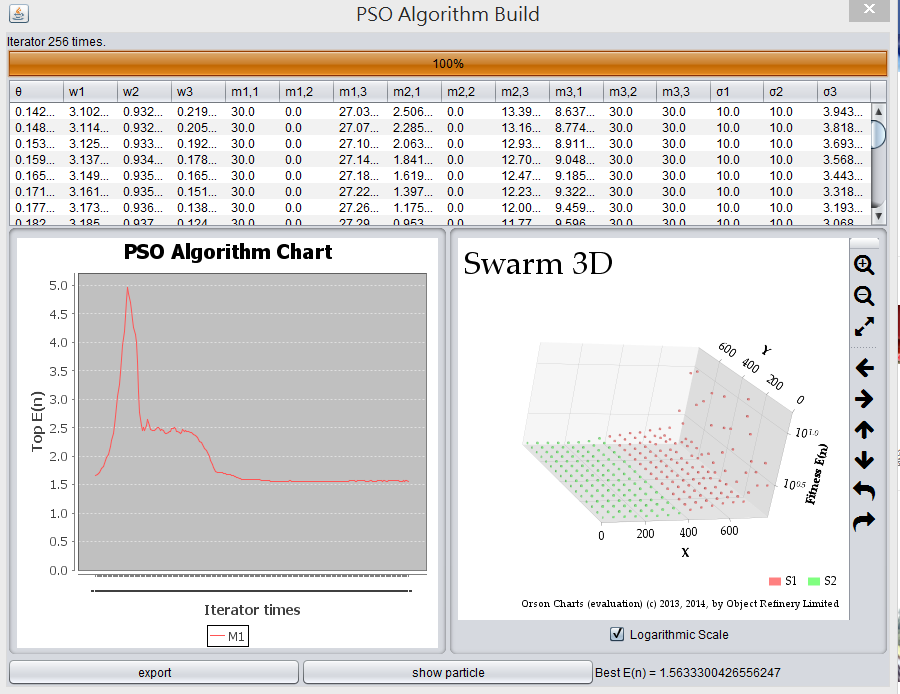
  • 其震盪的高低決定於鄰近模仿的權重，如果鄰近的粒子效果不好，模仿的權重高的時候，會導致整個最佳解有嚴重的偏離。由 PSO 3 中可以驗證這個震盪問題。

  • 如果對於全局模仿權重調高，很容易造成處於群聚粒子不容易分離，也就是很難在早到其他的區域最佳解，會在很快的時間內進入某一個區域最佳解，從這一點中可以發現 PSO 真的具有快速收斂的性質。

  • 設定 maxVelocity 是將整個向量長度 (歐幾里得距離) 壓縮，這將可以控制查找的精密度，如果設定太小會導致收斂速度明顯下降。將 maxVelocity = 10 時，適應函數看起來會有比較高的進展，由於會將每個參數約束，只要速度不是太小影響就不大。

  • 當速度上限增加時，粒子碰到牆的機會也會上升，由於搜索範圍的可能性涵蓋邊界的情況增加，如果最佳解在邊界，在這樣的情況就會更好。

  • 在代碼中，鄰近的定義為最近粒子中排名前 20% 的最佳解。如果採用對於常數長度，這種情況上不容易觀察，也就是說不能直接找到鄰近模仿的規模該定義在何處。

  • 運行結果 J = 3, p = 3
    ( ,w1 , w2 ,.., wJ , m11, m12,.., m1p, m21, m22,.., m2p,.., mJ1, mJ2,…, mJp, σ1, σ2, …, σJ) = (0.117271 1.270048 0.000000 0.805823 15.845525 0.000000 21.613452 13.509075 0.000000 0.000000 30.000000 0.000000 10.505934 10.000000 10.000000 5.238101)

Github Download

Download

Blog