解題區/解題區 - UVa

UVa 157 - Route Finding

contents

  1. 1. Problem
  2. 2. Input
  3. 3. Output
  4. 4. Sample input
  5. 5. Sample output
  6. 6. Solution

Problem

Many cities provide a comprehensive public transport system, often integrating bus routes, suburban commuter train services and underground railways. Routes on such systems can be categorised according to the stations or stops along them. We conventionally think of them as forming lines (where the vehicle shuttles from one end of the route to the other and returns), loops (where the two ends of the branch are the same and vehicles circle the system in both directions) and connections, where each end of the route connects with another route. Obviously all of these can be thought of as very similar, and can connect with each other at various points along their routes. Note that vehicles can travel in both directions along all routes, and that it is only possible to change between routes at connecting stations.

To simplify matters, each route is given a designation letter from the set A to Z, and each station along a route will be designated by another letter from the set a to z. Connecting stations will have more than one designation. Thus an example could be:

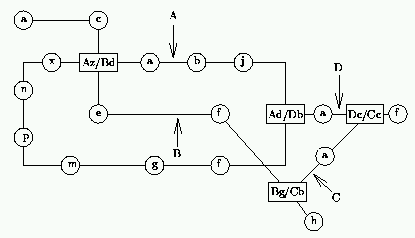
A common problem in such systems is finding a route between two stations. Once this has been done we wish to find the best route, where best means shortest time.

Write a program that will read in details of such a system and then will find the fastest routes between given pairs of stations. You can assume that the trip between stations always takes 1 unit of time and that changing between routes at a connecting station takes 3 units of time.

Input

Input will consist of two parts. The first will consist of a description of a system, the second will consist of pairs of stations. The description will start with a number between 1 and 26 indicating how many routes there are in the system. This will be followed by that many lines, each describing a single route. Each line will start with the route identifier followed by a : followed by the stations along that route, in order. Connections will be indicated by an = sign followed by the complete alternative designation. All connections will be identified at least once, and if there are more than two lines meeting at a connection, some or of all the alternative designations may be identified together. That is, there may be sequences such as ...hc=Bg=Cc=Abd.... If the route forms a loop then the last station will be the same as the first. This is the only situation in which station letters will be repeated. The next portion of the input file will consist of a sequence of lines each containing two stations written contiguously. The file will be terminated by a line consisting of a single #.

Output

Output will consist of a series of lines, one for each pair of stations in the input. Each line will consist of the time for the fastest route joining the two stations, right justified in a field of width 3, followed by a colon and a space and the sequence of stations representing the shortest journey. Follow the example shown below. Note that there will always be only one fastest route for any given pair of stations and that the route must start and finish at the named stations (not at any synonyms thereof), hence the time for the route must include the time for any inter-station transfers.

The example input below refers to the diagram given above.

Sample input

1
2
3
4
5
6
7
8
9
4
A:fgmpnxzabjd=Dbf
D:b=Adac=Ccf
B:acd=Azefg=Cbh
C:bac
AgAa
AbBh
BhDf
#

Sample output

1
2
3
 5: Agfdjba
 9: Abaz=Bdefgh
10: Bhg=Cbac=Dcf

Solution

題目描述：

這一個交通運輸工具，配置如上圖所述，以大寫字母 (A - Z) 表示哪一種線路，每一條線路上有一些站牌 (a - z)。求某線某站到某線某站的最少花費時間。

然而在同一個線路上，轉換一個站的成本為 1，如果在線路交集站換一條線路走成本為 3。

輸入上比較特別，會用 = 表示交集的站編號，當然有可能會遇到多個線路的站交集在一起。

Dhc=Bg=Cc=Abd 則表示 D 線路上的 Dh-Dc-Dd，其中 Dc, Bg, Cc, Ab 共站。

可以當作雙向連通，如果有環，則會頭尾相同，例如 Dhch。

題目解法：

題目最令人討厭的是，交集站沒有說清楚，也就是說單一線路上的轉運站沒有說清楚，但事實上會被表示在其他線路上，這裡要自己取聯集。

但是做聯集是件挺麻煩的事，因此在求最短路上做點手腳，把狀態表示成 (某線某站, 前一次是否轉運)，這麼做就方便多了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
#include <stdio.h>
#include <string.h>
#include <vector>
#include <queue>
using namespace std;
int trans_node(int r, int a) {
    r -= 'A', a -= 'a';
    return r * 26 + a;
}
void reverse_node(int n, int &r, int &a) {
    r = n /26 + 'A', a = n %26 + 'a';
}
vector<int> g[1024], g2[1024];
void spfa(int st, int ed) {
    int used[1024][2] = {}, dist[1024][2] = {}, prex[1024][2][2];
    for(int i = 0; i < 1024; i++)
        dist[i][0] = dist[i][1] = 0x3f3f3f3f;
    queue<int> Q, S;
    Q.push(st), S.push(0);
    dist[st][0] = 0, prex[st][0][0] = -1;
    while(!Q.empty()) {
        int u = Q.front(), s = S.front();
        Q.pop(), S.pop();
        used[u][s] = 0;
        for(int i = 0; i < g[u].size(); i++) {
            int v = g[u][i];
            if(dist[v][0] > dist[u][s] + 1) {
                dist[v][0] = dist[u][s] + 1;
                prex[v][0][0] = u, prex[v][0][1] = s;
                if(!used[v][0]) {
                    used[v][0] = 1, Q.push(v), S.push(0);
                }
            }
        }
        int cost = (s == 1) ? 0 : 3;
        for(int i = 0; i < g2[u].size(); i++) {
            int v = g2[u][i];
            if(dist[v][1] > dist[u][s] + cost) {
                dist[v][1] = dist[u][s] + cost;
                
                if(cost == 0)
                    prex[v][1][0] = prex[u][s][0], prex[v][1][1] = prex[u][s][1];
                else
                    prex[v][1][0] = u, prex[v][1][1] = s;
                if(!used[v][1]) {
                    used[v][1] = 1, Q.push(v), S.push(1);
                }
            }
        }
    }
    printf("%3d: ", min(dist[ed][0], dist[ed][1]));
    
    int r = -1, a = -1, s, mm = ed;
    if(dist[ed][0] <= dist[ed][1])
        s = 0;
    else
        s = 1;
    do {
        int nr, na;
        reverse_node(mm, nr, na);
        if(nr != r) {
            if(mm != ed)	printf("=");
            printf("%c%c", nr, na);
        } else {
            printf("%c", na);
        }
        int om = mm;
        mm = prex[om][s][0], s = prex[om][s][1];
        r = nr, a = na;
    } while(mm != -1);
    puts("");
}
int main() {
    char line[1024];
    for(int n; scanf("%d", &n) == 1;) {
        for(int i = 0; i < 1024; i++)
            g[i].clear(), g2[i].clear();
        while(n--) {
            scanf("%s", &line);
            int r = line[0], preX;
            preX = trans_node(r, line[2]);
            for(int i = 3; line[i]; i++) {
                if(line[i] != '=') {
                    int x = trans_node(r, line[i]);
                    int y = preX;
                    g[x].push_back(y);
                    g[y].push_back(x);
                    preX = x;
                } else {
                    int x = trans_node(line[i+1], line[i+2]);
                    int y = preX;
                    g2[x].push_back(y);
                    g2[y].push_back(x);
                    i += 2;
                }
            }
        }
        while(scanf("%s", line) == 1 && line[0] != '#') {
            int x = trans_node(line[0], line[1]);
            int y = trans_node(line[2], line[3]);
            spfa(y, x);
        }
    }
    return 0;
}
/*
4
A:fgmpnxzabjd=Dbf
D:b=Adac=Ccf
B:acd=Azefg=Cbh
C:bac
AgAa
AbBh
BhDf
#
5 
A:ab=Bbcdefghijk 
B:abc=Ajdef=Cb 
C:ab 
D:cd=Eg 
E:fg=Bf 
AaAk 
AcAk 
AbBb 
BaDd 
# 
*/