2014-07-06

UVa 11722 - Joining with Friend

1. Problem
2. Input
3. Output
4. Sample Input
5. Output for Sample Input
6. Solution

Problem

You are going from Dhaka to Chittagong by train and you came to know one of your old friends is going from city Chittagong to Sylhet. You also know that both the trains will have a stoppage at junction Akhaura at almost same time. You wanted to see your friend there. But the system of the country is not that good. The times of reaching to Akhaura for both trains are not fixed. In fact your train can reach in any time within the interval [t1, t2] with equal probability. The other one will reach in any time within the interval [s1, s2] with equal probability. Each of the trains will stop for w minutes after reaching the junction. You can only see your friend, if in some time both of the trains is present in the station. Find the probability that you can see your friend.

Input

The first line of input will denote the number of cases T (T < 500). Each of the following T line will contain 5 integers t1, t2, s1, s2, w (360 ≤ t1 < t2 < 1080, 360 ≤ s1 < s2 < 1080 and 1 ≤ w ≤ 90). All inputs t1, t2, s1, s2 and w are given in minutes and t1, t2, s1, s2 are minutes since midnight 00:00.

Output

For each test case print one line of output in the format “Case #k: p” Here k is the case number and p is the probability of seeing your friend. Up to 1e-6 error in your output will be acceptable.

Sample Input

1
2
3

2
1000 1040 1000 1040 20
720 750 730 760 16

Output for Sample Input

1 2	Case #1: 0.75000000 Case #2: 0.67111111

Solution

題目描述：

有兩位朋友，分別在 [t1, t2] 和 [s1, s2] 之間內可能會抵達，並且在那邊最多停留 w 單位時間。

問兩個人碰面的機率為何。

題目解法：

將兩個人分別至於 X Y 軸，利用幾何面積找到概率。

對於面積 [t1, t2]x[s1, s2] 只要符合 |t - s| <= w 的面積比例。

由於排容上可能不好理解，直接套用凸包交集的算法，兩個凸包交一定也是凸包。

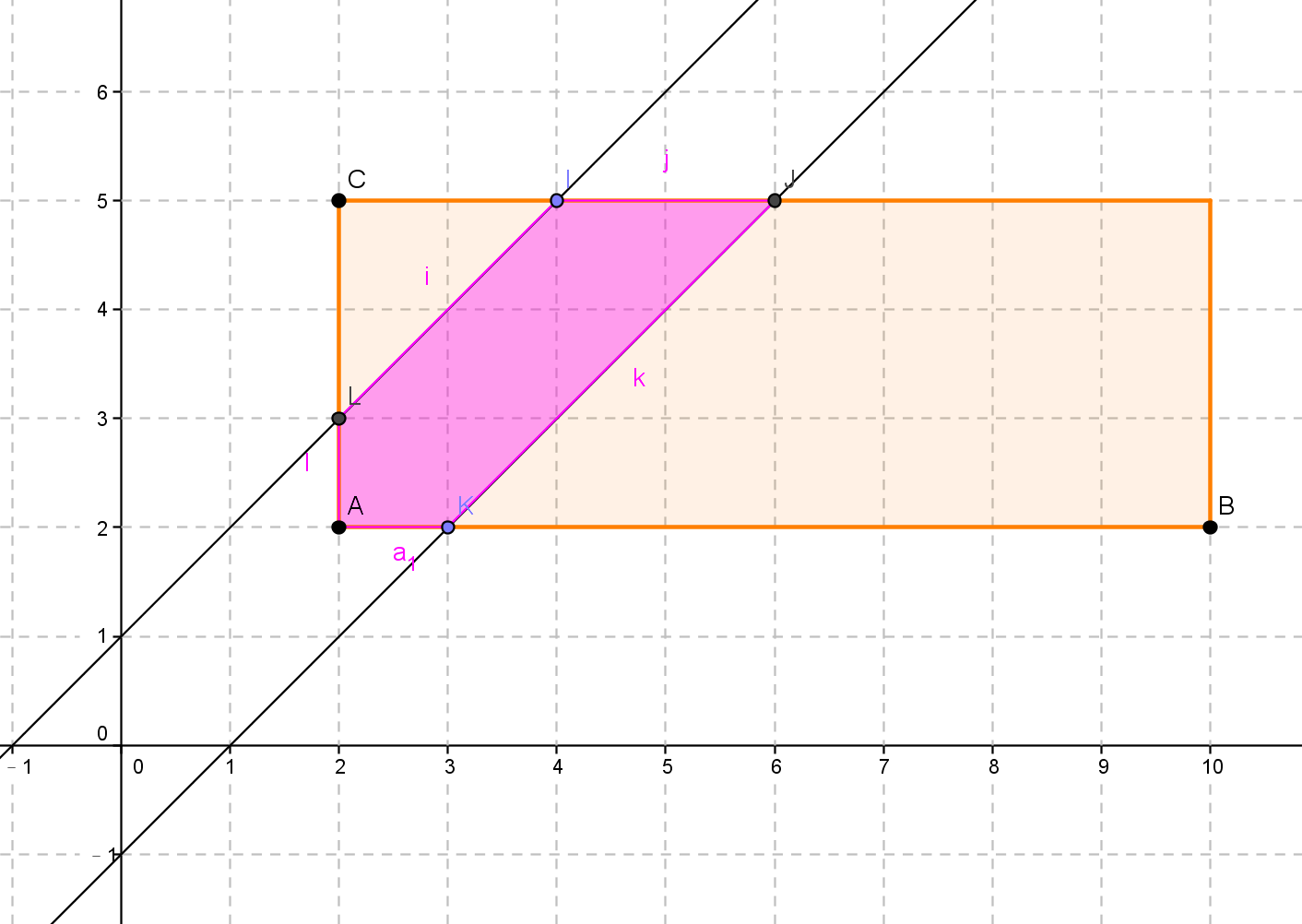
#include <stdio.h>
#include <math.h>
#include <algorithm>
using namespace std;
#define eps 1e-8
struct Pt {
    double x, y;
    Pt(double a = 0, double b = 0):
    	x(a), y(b) {}
    bool operator<(const Pt &a) const {
        if(fabs(x-a.x) > eps)	return x < a.x;
        return y < a.y;
    }
    bool operator==(const Pt &a) const {
        return fabs(x-a.x) < eps && fabs(y-a.y) < eps;
    }
    Pt operator+(const Pt &a) const {
        return Pt(x + a.x, y + a.y);
    }
    Pt operator-(const Pt &a) const {
        return Pt(x - a.x, y - a.y);
    }
    Pt operator/(const double val) const {
        return Pt(x / val, y / val);
    }
    Pt operator*(const double val) const {
        return Pt(x * val, y * val);
    }
};
typedef Pt Vector;
double dist(Pt a, Pt b) {
    return hypot(a.x - b.x, a.y - b.y);
}
double dot(Pt a, Pt b) {
    return a.x * b.x + a.y * b.y;
}
double cross2(Pt a, Pt b) {
    return a.x * b.y - a.y * b.x;
}
double cross(Pt o, Pt a, Pt b) {
    return (a.x-o.x)*(b.y-o.y)-(a.y-o.y)*(b.x-o.x);
}
int between(Pt a, Pt b, Pt c) {
    return dot(c - a, b - a) >= 0 && dot(c - b, a - b) >= 0;
}
int onSeg(Pt a, Pt b, Pt c) {
    return between(a, b, c) && fabs(cross(a, b, c)) < eps;
}
struct Seg {
    Pt s, e;
};
int calcIntersection(Seg a, Seg b, Pt &p) {
    double a1, b1, c1, a2, b2, c2;
    double d, dx, dy;
    a1 = a.s.y-a.e.y, b1 = -a.s.x+a.e.x;
    a2 = b.s.y-b.e.y, b2 = -b.s.x+b.e.x;
    c1 = a1*a.s.x + b1*a.s.y;
    c2 = a2*b.s.x + b2*b.s.y;
    d = a1*b2 - a2*b1;
    dx = c1*b2 - c2*b1;
    dy = a1*c2 - a2*c1;
    if(fabs(d) < eps) // NONE or LINE
        return 0;
    p.x = dx / d, p.y = dy / d;
    /*printf("%lf %lf - %lf %lf\n", a.s.x, a.s.y, a.e.x, a.e.y);
    printf("%lf %lf - %lf %lf\n", b.s.x, b.s.y, b.e.x, b.e.y);
    printf("%lf %lf\n", p.x, p.y);*/
    return onSeg(a.s, a.e, p) && onSeg(b.s, b.e, p);
}
int inPolygon(Pt p[], int n, Pt q) {
    int i, j, cnt = 0;
    for(i = 0, j = n-1; i < n; j = i++) {
        if(p[i].y > q.y != p[j].y > q.y &&
           q.x < (p[j].x-p[i].x)*(q.y-p[i].y)/(p[j].y-p[i].y) + p[i].x)
           cnt++;
    }
    return cnt&1;
}
double calcArea(Pt p[], int n) {
    if(n < 3)   return 0.0;
    double ret = 0;
    int i;
    p[n] = p[0];
    for(i = 0; i < n; i++)
        ret += p[i].x * p[i+1].y - p[i].y * p[i+1].x;
    return fabs(ret)/2;
}
int monotone(int n, Pt p[], Pt ch[]) {
    sort(p, p+n);
    int i, m = 0, t;
    for(i = 0; i < n; i++) {
        while(m >= 2 && cross(ch[m-2], ch[m-1], p[i]) <= 0)
            m--;
        ch[m++] = p[i];
    }
    for(i = n-1, t = m+1; i >= 0; i--) {
        while(m >= t && cross(ch[m-2], ch[m-1], p[i]) <= 0)
            m--;
        ch[m++] = p[i];
    }
    return m-1;
}
int main() {
    Pt a[64], b[64], ret[64], ch[64];
    int testcase, cases = 0;
    scanf("%d", &testcase);
    while(testcase--) {
    	int t1, t2, s1, s2, w;
    	int n = 4, m = 4, q;
    	scanf("%d %d %d %d %d", &t1, &t2, &s1, &s2, &w);
    	a[0] = Pt(t1, s1), a[1] = Pt(t2, s1);
    	a[2] = Pt(t2, s2), a[3] = Pt(t1, s2);
    	b[0] = Pt(0, w), b[1] = Pt(0, -w);
    	b[2] = Pt(t2, t2-w), b[3] = Pt(t2, t2+w);
        Seg seg1, seg2;
        int retN = 0;
        for(int i = 0, j = n-1; i < n; j = i++) {
            seg1.s = a[i], seg1.e = a[j];
            for(int p = 0, q = m-1; p < m; q = p++) {
                seg2.s = b[p], seg2.e = b[q];
                if(calcIntersection(seg1, seg2, ret[retN])) {
                    retN++;
                    /*printf("%lf %lf - %lf %lf\n", s1.s.x, s1.s.y, s1.e.x, s1.e.y);
                    printf("%lf %lf - %lf %lf +++\n", s2.s.x, s2.s.y, s2.e.x, s2.e.y);*/
                }
            }
        }
        for(int i = 0; i < n; i++)
            if(inPolygon(b, m, a[i]))
                ret[retN++] = a[i];
        for(int i = 0; i < m; i++)
            if(inPolygon(a, n, b[i]))
                ret[retN++] = b[i];
        q = monotone(retN, ret, ch);
        double area = calcArea(ch, q);
        printf("Case #%d: %.8lf\n", ++cases, area / ((t2 - t1) * (s2 - s1)));
    }
    return 0;
}

Morris' Blog