contents
前情提要 pbrt
一套數位影像生成軟體,盡可能以物理性質為基底打造的,目前已經到了 pbrt-v3。pbrt 主要的工作在於 modeling 後,可以在場景內放置以幾何描述的物體、光源、拍攝曝光 … 等設定,藉由模擬光線走訪得到呈現在螢幕上每一個 pixel 的顏色。
目標工作
Height Field 是一個高度場,測資中以山脈構造為主,等間隔取樣每一平面上的每一點高度的場景,當間隔越小越接近真實場景。原生寫法是將點放置在三維空間,轉換成一堆三角網格,將其丟入 KD-tree 或者是 BVH 等加速結構,加快光線模擬找交點 (三維空間中,一射線和一多面體的交點) 的效能。而現在挑戰用 3D-DDA 的方式進行交點查找。
實作採用 3D-DDA 算法降至 2D Grid 上進行交點測試。Uniform Grid 將會切割成 $N \times M$ 的格子,在 2D 平面上,先找到 ray 進入的格子點,接著使用增量算法找到下一個格子,算法只測試投影到 x-y 平面上時,在 ray 鄰近的格子點做交點測試,時間複雜度 $O(\sqrt{N \times M})$,與預設的其他算法所需要的 traversal 複雜度差不多。
原本預設的 Height Field 拆成好幾個 Triangle,做法類似 Triangle Mesh,接著將這幾個 Triangle 利用 BVH 或者是 KD-tree 的架構進行,原本的做法會考慮三個維度,使用投影的方式只考慮兩個維度下的情況,接著再針對有相交的格子測試,最後才進行 3D Triangle 是否與 ray 相交。
實作 Height Field 時,考慮快取和再計算之間的好壞,則有兩種方法
- 預先將預處理每個 3D Triangle 座標 (消耗空間)
- 需要時,再創建 Triangle 出來測試 (消耗時間)
由於要找 ray 碰度到 uniform grid 的第一個格子,需要預處理 Height Field Bound Box,計算 Bound Box 需要 $O(N \times M)$,若不預處理會造成 3D-DDA 與暴力法 $O(N \times M)$ 無異。
若對 Height Field 進行 2D-DDA 好處在於一定是數個三角形構成,因此不用等到 ray.maxT 小於下一格交點的 NextCrossingT[stepAxis] 才能結束,一與三角形有交點就可以離開,因為每一格之間都有獨立性。
實作與測試細節
測試環境
一開始為了熟悉 pbrt 架構環境只實作求出交點的函數,
|
|
而直接忽略單純詢問交點是否存在,這會導致畫面一片黑,因為每打到一個交點會嘗試從物體表面的交點連到點光源。若下述函數恆真,則不存在光源到交點的路徑,因此產出來的圖片是一片黑。
|
|
紋理模糊
找出紋理的兩個參數 $(u, v)$ 時,從 trianglemesh.cpp 複製過來的 class Triangle 其 bool Triangle::Intersect() 函數得到的 $u, v$ 都是相對於三角形的 $0 \le u, v \le 1$ (直接 rendering 會看起來很多小格子點),因此得到相對的 $u, v$ 和交點 $p_{hit}$ (Object coordinate),則把 $p_{hit}$ 再次投影到 x-y 平面上,由於 height field 在 x-y 平面上長寬都是 1,投影到平面後得到 $p_{projection}$,對於整個 height field $u = p_{projection}.x, \; v = p_{projection}.y$。
若測試 texture.pbrt 時,發生過模糊情況,其主要原因在於過多次座標轉換,如
Object -> World -> Object -> World,求出來的 $u, v$ 誤差就會放大。
將 height field 存成好幾個 triangle 可以像 class TriangleMesh 利用 index 標籤來壓縮記憶體,但實作為方便仍然每一個三角形都有實體的 Point,儲存三角形每一個點座標採用 object coordinate,先把 $ray$ 從 WorldToObject 得到 $ray'$,得到的交點 $p_{hit}$ 再進行 ObjectToWorld,如此一來模糊情況就會消失。
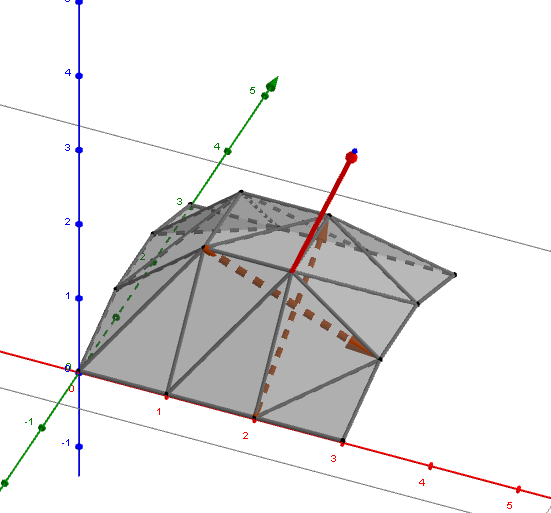
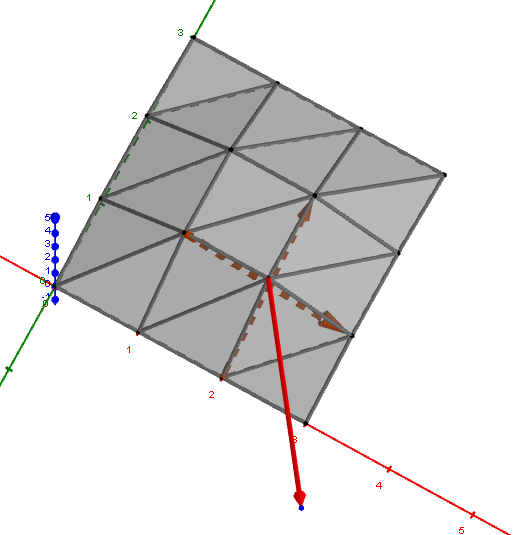
Phong 圓滑化
Phong interpolation 方法在三角形上面操作時,需要得知三個頂點的法向量,給予 height field 的資訊,並不曉得每一個頂點的法向量為何。得到每一個頂點的法向量,採用預先處理所有頂點的法向量並儲存起來,因為不斷地正規化是很耗時間的 (float sqrt(float x) 儘管採用 fast inverse square root 算法,也要極力避免多餘的運算)。
再計算頂點法向量時,根據影像處理中常用的一次差分 (differentiation) 遮罩
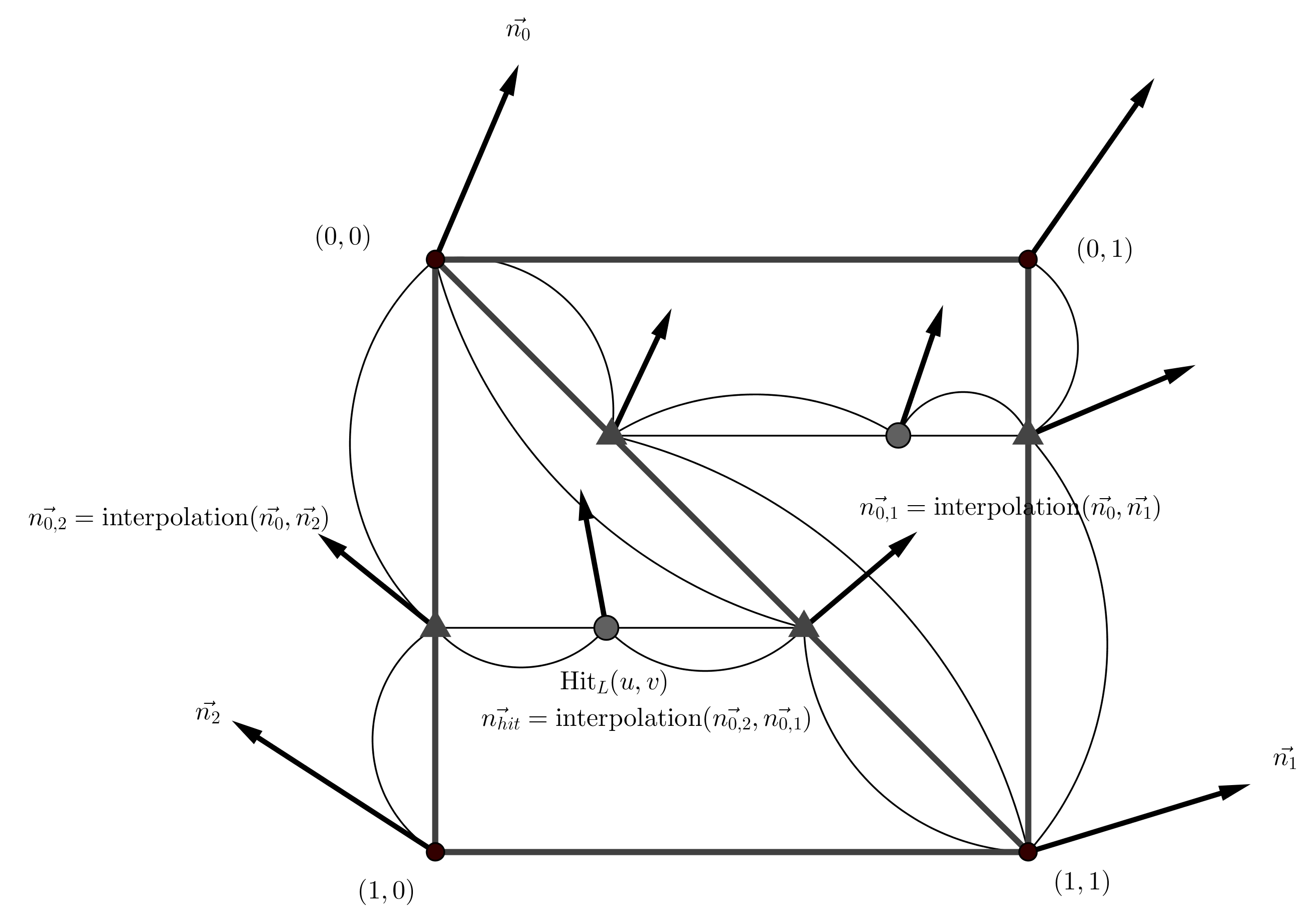
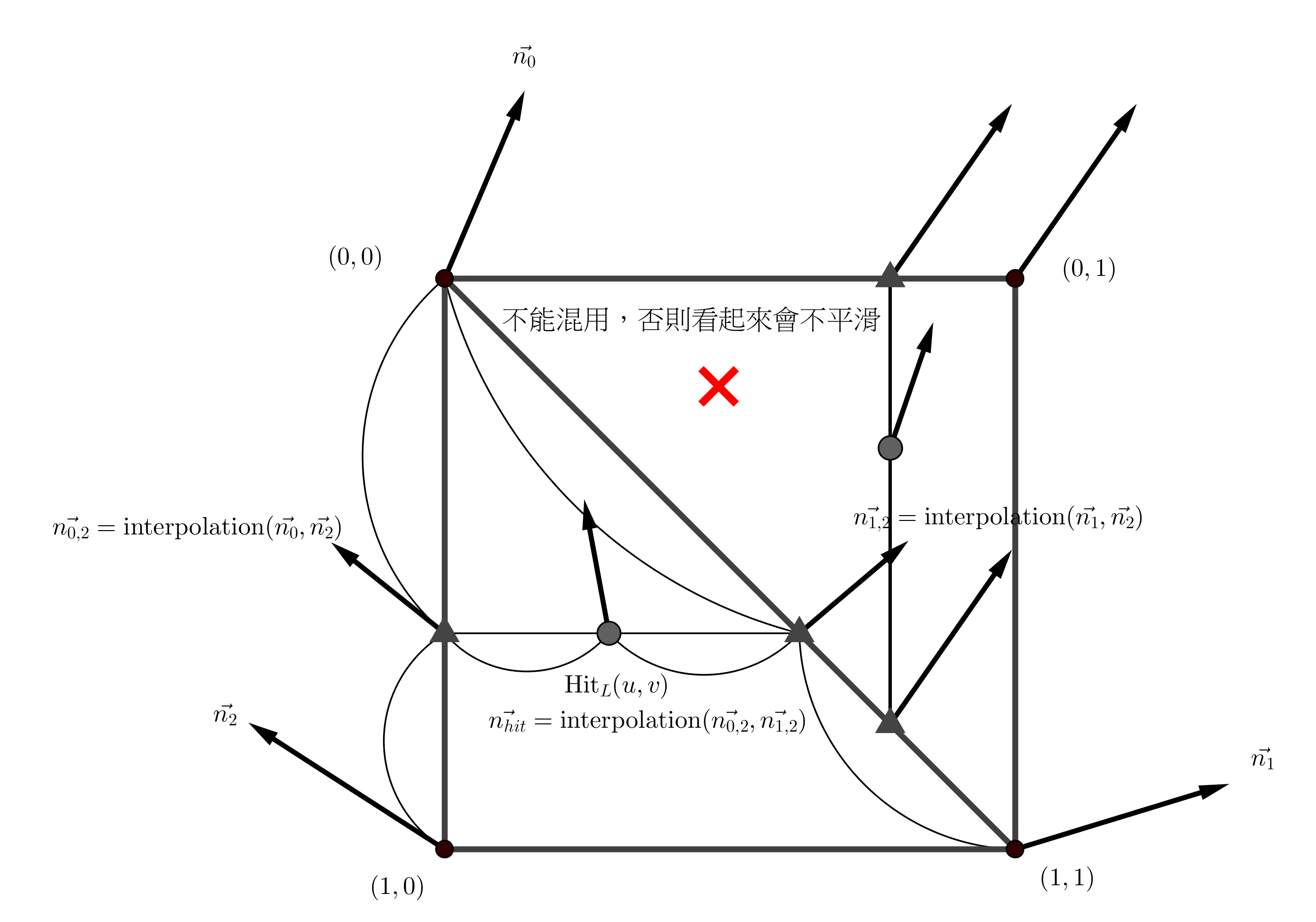
Case 1 邊緣
$$N_x = \begin{bmatrix} 0 & 0 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix}, \; N_y = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -1 & 0 \\ \end{bmatrix}$$Case 2 非邊緣
$$N_x = \begin{bmatrix} 0 & 0 & 0 \\ -1 & 0 & 1 \\ 0 & 0 & 0 \\ \end{bmatrix}, \; N_y = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & -1 & 0 \\ \end{bmatrix}$$上圖矩陣的中心座標為 $(x, y)$,將相鄰座標的高度值 $z$ 相減得到兩個方向的向量 $N_x, \; N_y$,外積得到座標 $(x, y)$ 的法向量 $N_{x, y} = \mathrm{Cross}(N_x, N_y)$。
從另一個角度來看,將 height field 三角化後,每一個頂點原則上有 6 個鄰居,可以對每一個鄰居進行差分,接著順時針或者逆時針將兩兩相臨的向量外積,得到 6 個法向量平均後得到 $N_{x, y}$,這做法看起來比上述的差分來得穩定,但初始化消耗的時間會比較長,且撰寫的外積順序不對容易造成零向量的正規化錯誤。
Final Images Rendered with my implementation of heightfield.cpp
 hftest.pbrt (without Phong Timings:
|  landsea-0.pbrt (without Phong Timings:
|
 landsea-1.pbrt (without Phong Timings:
|  landsea-2.pbrt (without Phong Timings:
|
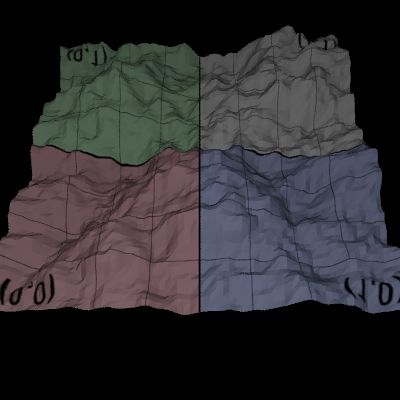 texture.pbrt (without Phong Timings:
| |
 landsea-big.pbrt (without Phong Timings:
| |
Final Images Rendered with my implementation of heightfield.cpp
 hftest.pbrt (with Phong Timings:
|  landsea-0.pbrt (with Phong Timings:
|
 landsea-1.pbrt (with Phong Timings:
|  landsea-2.pbrt (with Phong Timings:
|
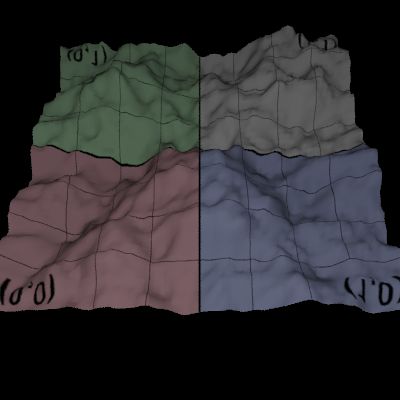 texture.pbrt (with Phong Timings:
| |
 landsea-big.pbrt (with Phong interpolation) Timings:
| |