contents
Ray Sphere Intersection
計算射線和球體的交點,可以參照 /pbrt-v2/shapes/sphere.cpp 中 bool Shpere::Intersect() 的算法。
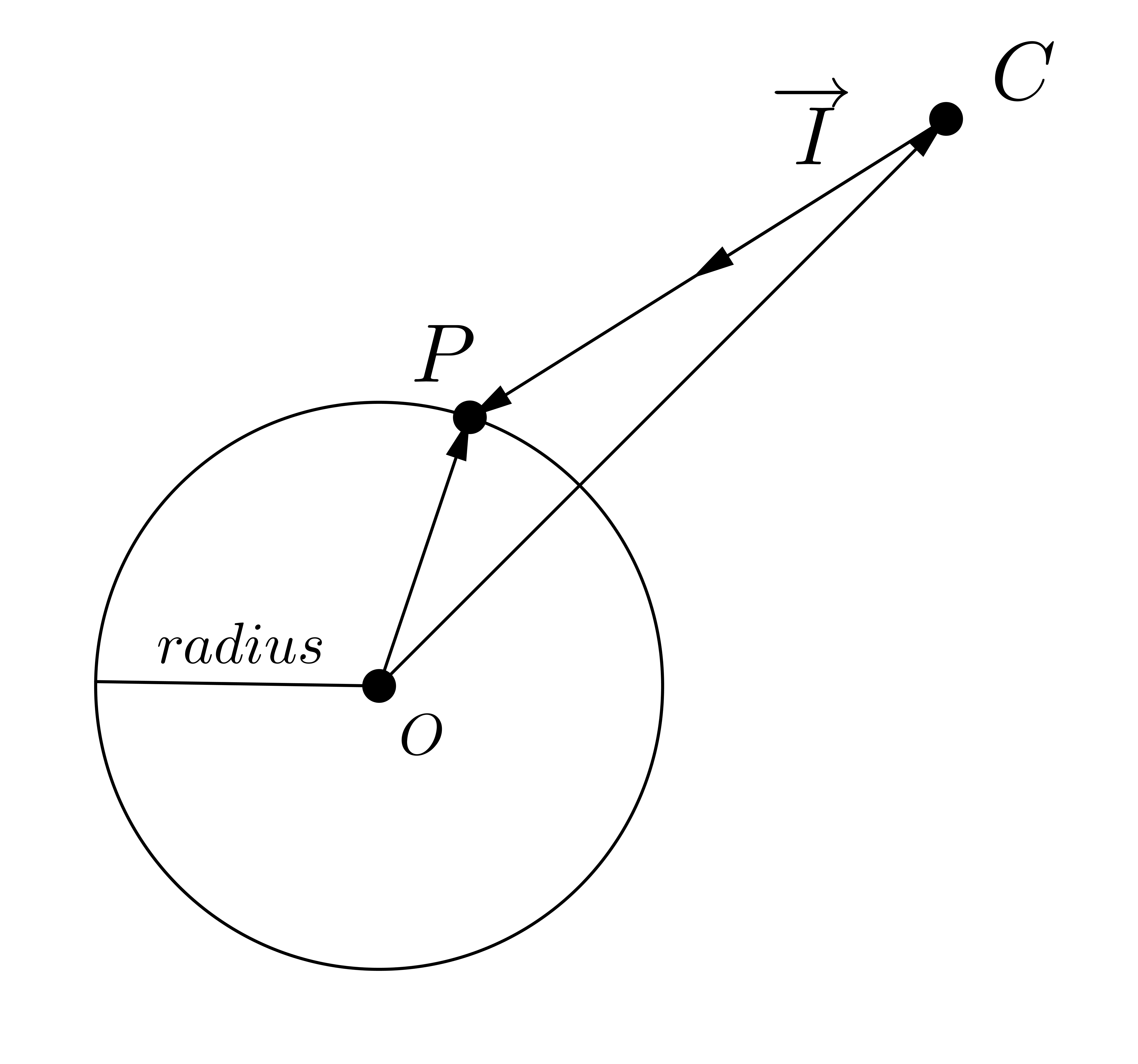
假設球體圓心座標 $O$,射線單位向量 $I$ 的起點座標 $C$,且最近目標交點座標 $P$,原半徑 $\mathrm{radius}$。射線走單位時間 $t$ 會到達球面上。
- $\overrightarrow{OC} + \overrightarrow{I} \times t = \overrightarrow{OP}$
- $|\overrightarrow{OP}| = \text{radius}$
- $|\overrightarrow{OC} + \overrightarrow{I} \times t| = |\overrightarrow{OP}|$
- $|\overrightarrow{I}|^2 t^2 + 2 \; (\overrightarrow{OC} \cdot \overrightarrow{I}) \; t + |\overrightarrow{OC}|^2 - \text{radius}^2 = 0$
解一元二次方程式之後可以得到 $t$ 得值,並得到交點座標 $P$。
Snell’s Law
根據物理法則斯乃爾定律計算折射的方向向量,課程中提供三種做法。
變數解釋:入射介面材質 $\eta_1$,折射介面材質 $\eta_2$,入射單位向量 $\overrightarrow{I}$,交點面法向量 $\overrightarrow{N}$,折射方向向量 $\overrightarrow{T}$
特別小心 ray->d = Normalize(ray->d) 的處理,Heckbert’s Method 計算維持在單位圓上,故不用做最後的正規化計算。
Whitted’s Method
| $\sqrt{}$ | $/$ | $\times$ | $+$ | compute |
|---|---|---|---|---|
| 1 | $n = \eta_1 / \eta_2$ | |||
| 3 | 3 | 2 | $I' = I / (-I \cdot N)$ | |
| 3 | $J = I' + N$ | |||
| 1 | 1 | 8 | 5 | $\alpha = 1 / \sqrt{n^2(I' \cdot I') - (J \cdot J)}$ |
| 3 | 3 | $T' = \alpha J - N$ | ||
| 1 | 3 | 3 | 2 | $T' = T' / \| T' \|$ |
| 2 | 8 | 17 | 15 | TOTAL |
Heckbert’s Method
| $\sqrt{}$ | $/$ | $\times$ | $+$ | compute |
|---|---|---|---|---|
| 1 | $\eta = \eta_1 / \eta_2$ | |||
| 3 | 2 | $c_1 = - I \cdot N$ | ||
| 1 | 3 | 2 | $c_2 = \sqrt{1 - \eta^2(1 - c_1^2)}$ | |
| 7 | 4 | $T = \eta I + (\eta c_1 - c_2) N$ | ||
| 1 | 1 | 13 | 8 | TOTAL |
Other Method
| $\sqrt{}$ | $/$ | $\times$ | $+$ | compute |
|---|---|---|---|---|
| 1 | $n = \eta_2 / \eta_1$ | |||
| 3 | 2 | $c_1 = - I \cdot N$ | ||
| 1 | 2 | 3 | $\beta = c_1 \sqrt{n^2 - 1 + c_1^2}$ | |
| 3 | 3 | 3 | $T = (I + \beta N ) / n$ | |
| 1 | 4 | 8 | 8 | TOTAL |
其中以 Heckbert’s Method 消耗最少計算數。如果除法速度快於乘法,則使用 Other Method,原則上很少有機器運算除法比乘法快。
RasterToCamera
這部分處理後得到 Transform RasterToCamera。若計算錯誤,會造成一片黑或者圖片顯示的大小問題。座標轉換處理細節可以參考實際的例子,如下圖所示:
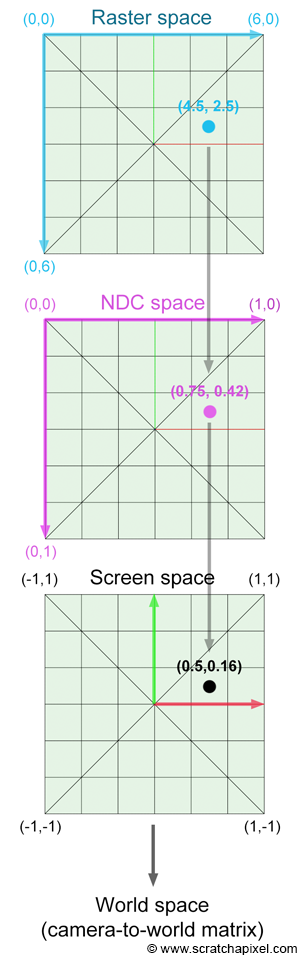
- Raster-To-NDC 轉換矩陣 $A=\text{Scale}(scale, scale, 1)$,進行縮放。
- NDC-To-Camera 轉換矩陣 $B=\text{Translate}(Vector(0, 0, filedistance)) \times \text{Translate}(Vector(X, -Y, 0))$,進行位移。
- 最後得到 RasterToCamera 轉換矩陣 $C= B \times A \times \text{Scale}(-1, 1, 1)$,最後將 x 軸顛倒以符合成像問題。
Ray Weight
作業要求經過 float GenerateRay() 回傳 $\mathrm{weight} = \frac{\cos^4 \theta'}{Z^2}$,這麼設置會過暗,根據論文 A Realistic Camera Model for Computer Graphics 中寫道
If the exit pupil subtends a small solid angle from $x'$, $\theta'$ can be assumed to be constant and equal the angle between $x'$ and the center of the disk. This allows us to simplify
$E(x') = \int_{x'' \in D} L(x'', x') \frac{\cos \theta' \cos \theta''}{\| x'' - x'\|} dA''$<span>$to:$</span><!-- Has MathJax -->$E(x’) = L \frac{A}{Z^2} \cos^4 \theta’$
where $Z$ is the axial distance from the film plane to the dist and $A$ is the area of the disk.
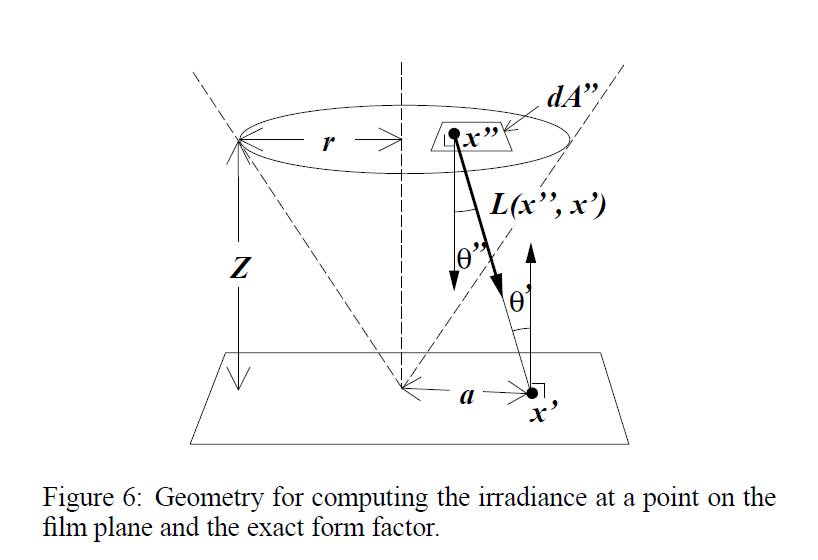
因此需要額外乘上常數 $A$,其中 $A$ 是最裡層的透鏡面積,因為我們是根據最裡層的透鏡面做均勻取樣,得到 $A = \mathit{backLens.radius}^2 \pi$。
Sampling
單位圓均勻取樣方法有以下兩種,而非均勻取樣的寫法可參照 Sample 3 (錯誤的做法參照) 出來的效果看出。
Sampling 1
採用內建函數 CencentricSampleDisk(),採用 A Low Distortion Map Between Disk and Square 論文中提到的方案,將一個正方形壓縮到一個圓形中。參照作法如下圖所示 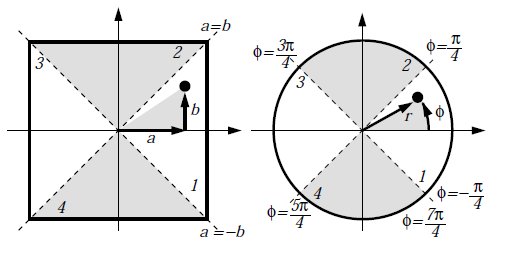
其中給定 $a, b$ 均勻分布 $[0, 1]$,則得到 $r = a, \; \phi = \frac{\pi}{4} \frac{b}{a}$,最後計算得到座標 $x = r \cos \phi, \; y = r \sin \phi$。
Sampling 2
採用教科書上提供,其中給定 $a, b$ 均勻分布 $[0, 1]$,令 $r = \sqrt{a}, \; \phi = 2 \pi b$,最後計算得到座標 $x = r \cos \phi, \; y = r \sin \phi$。
Sampling 3
分布 $[0, 1]$,令 $r = a, \; \phi = 2 \pi b$,最後計算得到座標 $x = r \cos \phi, \; y = r \sin \phi$。這種寫法在相同半徑下,角度均勻分布,不同半徑下的周長與 $r$ 成正比,導致不同半徑的取樣點不均勻,越靠近中心點取樣越密集,意即容易造成中心點看起來較亮。
Reference
Final Images Rendered Compare 4 samples
Gauss Lens
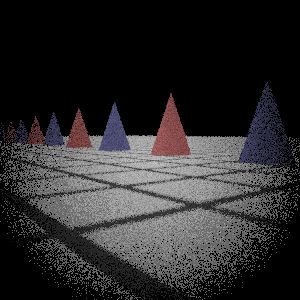 My Implementation (Sampling 1)
| 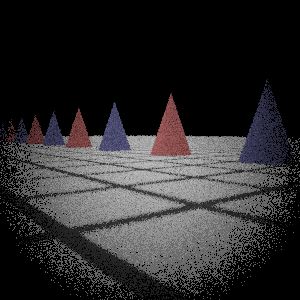 My Implementation (Sampling 2)
| 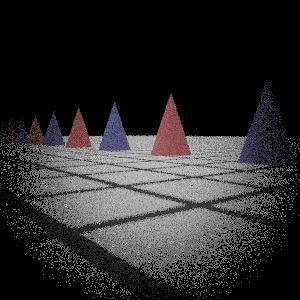 My Implementation (Sampling 3)
|
Fisheye Lens
 My Implementation (Sampling 1)
|  My Implementation (Sampling 2)
|  My Implementation (Sampling 3)
|
Telephoto Lens
 My Implementation (Sampling 1)
|  My Implementation (Sampling 2)
|  My Implementation (Sampling 3)
|
Wide-Angle Lens
 My Implementation (Sampling 1)
|  My Implementation (Sampling 2)
|  My Implementation (Sampling 3)
|
Final Images Rendered Compare 512 samples
Gauss Lens
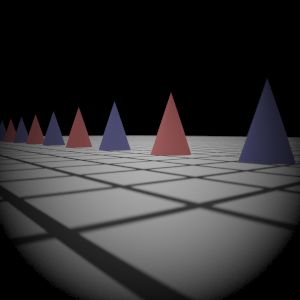 Reference
| 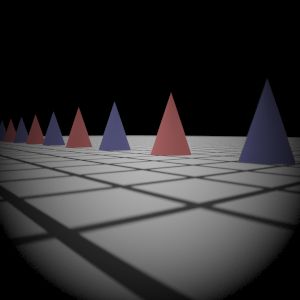 My Implementation (Sampling 1)
| 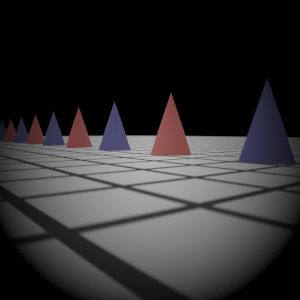 My Implementation (Sampling 2)
| 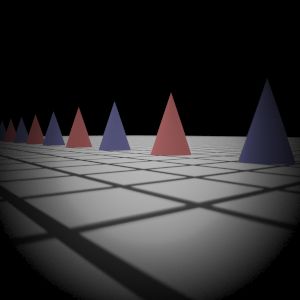 My Implementation (Sampling 3)
|
Fisheye Lens
 Reference
|  My Implementation (Sampling 1)
|  My Implementation (Sampling 2)
|  My Implementation (Sampling 3)
|
Telephoto Lens
 Reference
|  My Implementation (Sampling 1)
|  My Implementation (Sampling 2)
|  My Implementation (Sampling 3)
|
Wide-Angle Lens
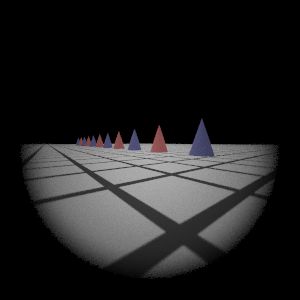 Reference
| 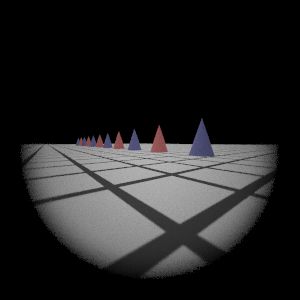 My Implementation (Sampling 1)
| 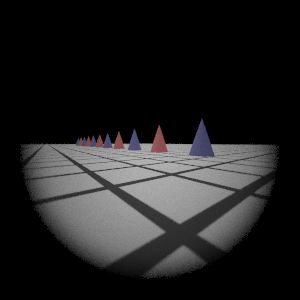 My Implementation (Sampling 2)
|  My Implementation (Sampling 3)
|