#include <stdio.h>
#include <math.h>
#include <algorithm>
using namespace std;
#define eps 1e-8
struct Pt {
double x, y;
Pt(double a = 0, double b = 0):
x(a), y(b) {}
bool operator<(const Pt &a) const {
if(fabs(x-a.x) > eps) return x < a.x;
return y < a.y;
}
bool operator==(const Pt &a) const {
return fabs(x-a.x) < eps && fabs(y-a.y) < eps;
}
Pt operator+(const Pt &a) const {
return Pt(x + a.x, y + a.y);
}
Pt operator-(const Pt &a) const {
return Pt(x - a.x, y - a.y);
}
Pt operator/(const double val) const {
return Pt(x / val, y / val);
}
Pt operator*(const double val) const {
return Pt(x * val, y * val);
}
};
typedef Pt Vector;
double dist(Pt a, Pt b) {
return hypot(a.x - b.x, a.y - b.y);
}
double dot(Pt a, Pt b) {
return a.x * b.x + a.y * b.y;
}
double cross2(Pt a, Pt b) {
return a.x * b.y - a.y * b.x;
}
double cross(Pt o, Pt a, Pt b) {
return (a.x-o.x)*(b.y-o.y)-(a.y-o.y)*(b.x-o.x);
}
int between(Pt a, Pt b, Pt c) {
return dot(c - a, b - a) >= 0 && dot(c - b, a - b) >= 0;
}
int onSeg(Pt a, Pt b, Pt c) {
return between(a, b, c) && fabs(cross(a, b, c)) < eps;
}
struct Seg {
Pt s, e;
};
int calcIntersection(Seg a, Seg b, Pt &p) {
double a1, b1, c1, a2, b2, c2;
double d, dx, dy;
a1 = a.s.y-a.e.y, b1 = -a.s.x+a.e.x;
a2 = b.s.y-b.e.y, b2 = -b.s.x+b.e.x;
c1 = a1*a.s.x + b1*a.s.y;
c2 = a2*b.s.x + b2*b.s.y;
d = a1*b2 - a2*b1;
dx = c1*b2 - c2*b1;
dy = a1*c2 - a2*c1;
if(fabs(d) < eps)
return 0;
p.x = dx / d, p.y = dy / d;
return onSeg(a.s, a.e, p) && onSeg(b.s, b.e, p);
}
int inPolygon(Pt p[], int n, Pt q) {
int i, j, cnt = 0;
for(i = 0, j = n-1; i < n; j = i++) {
if(p[i].y > q.y != p[j].y > q.y &&
q.x < (p[j].x-p[i].x)*(q.y-p[i].y)/(p[j].y-p[i].y) + p[i].x)
cnt++;
}
return cnt&1;
}
double calcArea(Pt p[], int n) {
if(n < 3) return 0.0;
double ret = 0;
int i;
p[n] = p[0];
for(i = 0; i < n; i++)
ret += p[i].x * p[i+1].y - p[i].y * p[i+1].x;
return fabs(ret)/2;
}
int monotone(int n, Pt p[], Pt ch[]) {
sort(p, p+n);
int i, m = 0, t;
for(i = 0; i < n; i++) {
while(m >= 2 && cross(ch[m-2], ch[m-1], p[i]) <= 0)
m--;
ch[m++] = p[i];
}
for(i = n-1, t = m+1; i >= 0; i--) {
while(m >= t && cross(ch[m-2], ch[m-1], p[i]) <= 0)
m--;
ch[m++] = p[i];
}
return m-1;
}
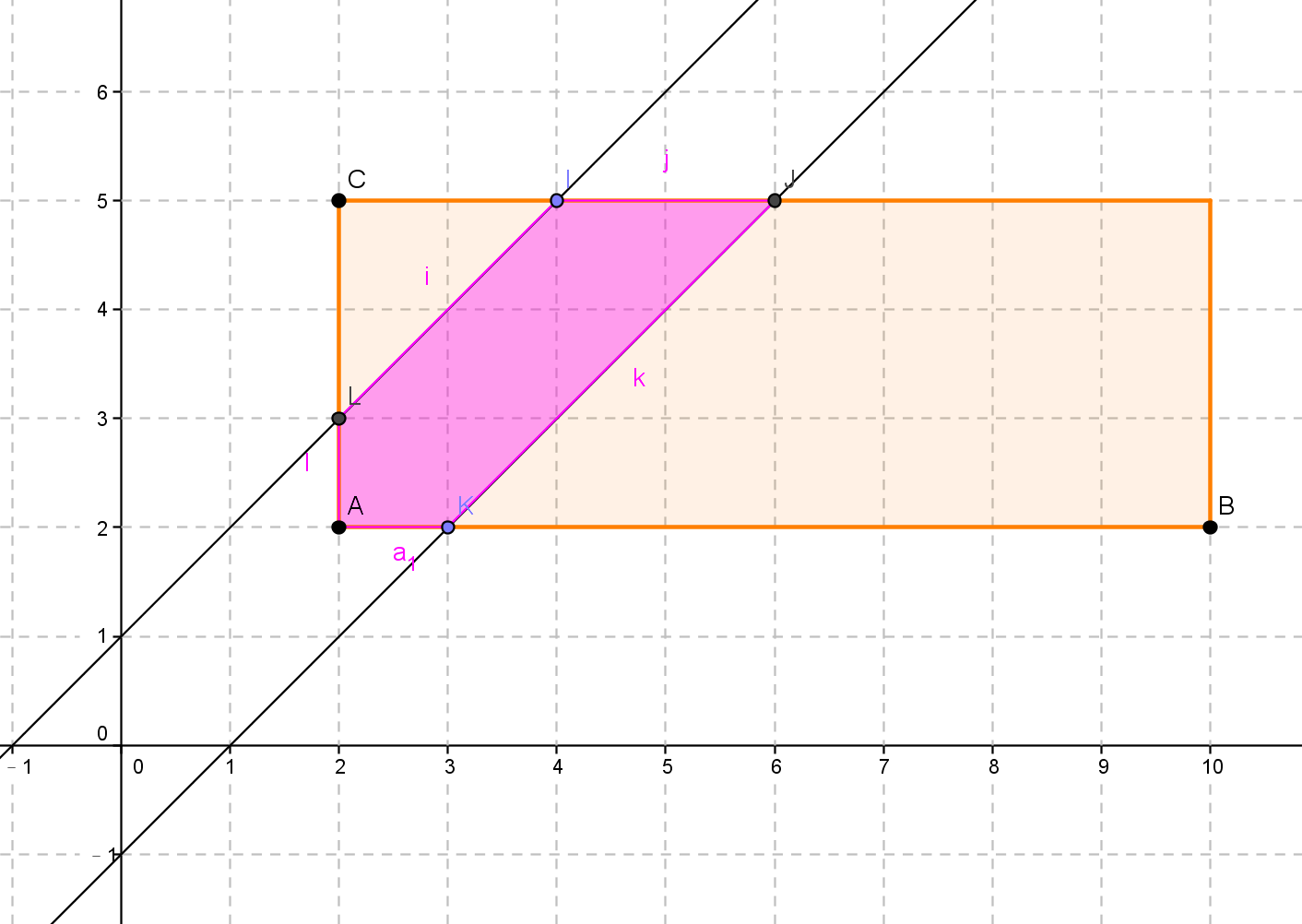
int main() {
Pt a[64], b[64], ret[64], ch[64];
int testcase, cases = 0;
scanf("%d", &testcase);
while(testcase--) {
int t1, t2, s1, s2, w;
int n = 4, m = 4, q;
scanf("%d %d %d %d %d", &t1, &t2, &s1, &s2, &w);
a[0] = Pt(t1, s1), a[1] = Pt(t2, s1);
a[2] = Pt(t2, s2), a[3] = Pt(t1, s2);
b[0] = Pt(0, w), b[1] = Pt(0, -w);
b[2] = Pt(t2, t2-w), b[3] = Pt(t2, t2+w);
Seg seg1, seg2;
int retN = 0;
for(int i = 0, j = n-1; i < n; j = i++) {
seg1.s = a[i], seg1.e = a[j];
for(int p = 0, q = m-1; p < m; q = p++) {
seg2.s = b[p], seg2.e = b[q];
if(calcIntersection(seg1, seg2, ret[retN])) {
retN++;
}
}
}
for(int i = 0; i < n; i++)
if(inPolygon(b, m, a[i]))
ret[retN++] = a[i];
for(int i = 0; i < m; i++)
if(inPolygon(a, n, b[i]))
ret[retN++] = b[i];
q = monotone(retN, ret, ch);
double area = calcArea(ch, q);
printf("Case #%d: %.8lf\n", ++cases, area / ((t2 - t1) * (s2 - s1)));
}
return 0;
}