解題區/解題區 - UVa

UVa 177 - Paper Folding

contents

  1. 1. Problem
  2. 2. Input
  3. 3. Output
  4. 4. Sample input
  5. 5. Sample output
  6. 6. Solution

Problem

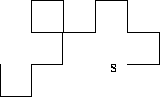
If a large sheet of paper is folded in half, then in half again, etc, with all the folds parallel, then opened up flat, there are a series of parallel creases, some pointing up and some down, dividing the paper into fractions of the original length. If the paper is only opened half-way'' up, so every crease forms a 90 degree angle, then (viewed end-on) it forms adragon curve’’. For example, if four successive folds are made, then the following curve is seen (note that it does not cross itself, but two corners touch):

UVa 177

Write a program to draw the curve which appears after N folds. The exact specification of the curve is as follows:

  • The paper starts flat, with the ``start edge’’ on the left, looking at it from above.
  • The right half is folded over so it lies on top of the left half, then the right half of the new double sheet is folded on top of the left, to form a 4-thick sheet, and so on, for N folds.
  • Then every fold is opened from a 180 degree bend to a 90 degree bend.
  • Finally the bottom edge of the paper is viewed end-on to see the dragon curve.

From this view, the only unchanged part of the original paper is the piece containing the start edge, and this piece will be horizontal, with the start edge on the left. This uniquely defines the curve. In the above picture, the start edge is the left end of the rightmost bottom horizontal piece (marked s). Horizontal pieces are to be displayed with the underscore character _, and vertical pieces with the | character.

Input

Input will consist of a series of lines, each with a single number N (1 <= N <= 13). The end of the input will be marked by a line containing a zero.

Output

Output will consist of a series of dragon curves, one for each value of N in the input. Your picture must be shifted as far left, and as high as possible. Note that for large N, the picture will be greater than 80 characters wide, so it will look messy on the screen. The pattern for each different number of folds is terminated by a line containing a single `^’.

Sample input

1
2
3
4
2
4
1
0

Sample output

1
2
3
4
5
6
7
8
9
10
|_
 _|
^
   _   _
  |_|_| |_
   _|    _|
|_|
^
_|
^

Solution

題目描述：

將一個長條紙水平擺放，接著將右手邊的紙摺疊到左上邊的紙上面，接著又再重複做幾次，直到 N 次 ( 若將其攤平則會有 2N 個折疊區塊 )。摺疊完後，依序將其攤開，攤開的方式為：將前一次摺疊的 (想像與 s 重疊的那一片) 從 180 度旋轉到 90 度位置，依序攤開 N 次。

題目解法：

這一題就是題目理解麻煩點，但是不難發現肯定是有遞迴需要處理的。

假設我們定義展開的每一根，分別為往上下左右的射線，會發現其對應關係，新的尾會跟舊的頭對照，依序對照到中間部分。

最後得到關係

  • 上 變成 左
  • 下 變成 右
  • 左 變成 下
  • 右 變成 上

輸出處理方面，利用一個 map 結構去完成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include <stdio.h> 
#include <map>
#include <set>
#include <algorithm>
using namespace std;
map<int, set< pair<int, int> > > P;
void build(int n) {
    int A[1<<15];
    // 0 up, 1 down, 2 left, 3 right
    int trans[] = {2, 3, 1, 0};
    int m = 1;
    A[0] = 3;
    for(int i = 1; i <= n; i++) {
        for(int j = m - 1, k = m; j >= 0; j--, k++)
            A[k] = trans[A[j]];
        m = m << 1;
    }
    int x = -1, y = 0, px = 0, py = 0;
    P.clear();
    for(int i = 0; i < m; i++) {
        if(A[i] == 0)		x = px<<1, y = py;
        else if(A[i] == 1)	x = px<<1, y = py - 1;
        else if(A[i] == 2)	x = (px<<1)-1, y = py;
        else				x = (px<<1)+1, y = py;
        //printf("%d %d %d - %d %d\n", px, py, A[i], x, y);
        if(A[i] == 0) {
            P[y].insert(make_pair(x, 0));
        } else if(A[i] == 1) {
            P[y].insert(make_pair(x, 1));
        } else if(A[i] == 2) {
            P[y].insert(make_pair(x, 2));
        } else {
            P[y].insert(make_pair(x, 3));
        }
        if(A[i] == 0)		py++;
        else if(A[i] == 1)	py--;
        else if(A[i] == 2)	px--;
        else				px++;
    }
}
int main() {
    for(int n; scanf("%d", &n) == 1 && n; ) {
        build(n);
        int mxy = -0x3f3f3f3f, mnx = 0x3f3f3f3f;
        for(map<int, set< pair<int, int> > >::iterator it = P.begin();
        it != P.end(); it++) {
            mxy = max(mxy, it->first);
            for(set< pair<int, int> >::iterator jt = it->second.begin();
                jt != it->second.end(); jt++) {
                mnx = min(mnx, jt->first);
            }
        }
        for(map<int, set< pair<int, int> > >::reverse_iterator it = P.rbegin();
        it != P.rend(); it++) {
            int i = mnx;
            for(set< pair<int, int> >::iterator jt = it->second.begin();
                jt != it->second.end(); jt++) {
                while(i < jt->first)	putchar(' '), i++;
                i++;
                if(jt->second == 0 || jt->second == 1)
                    putchar('|');
                else
                    putchar('_');
            }
            puts("");
        }
        //printf("%d %d\n", mxy, mnx);
        puts("^");
    }
    return 0;
}