編譯器 Compiler CFG LL(1)

序文

相較於其他技術而言，編譯器的確不是什麼有趣的課程，在這一門領域專研的人也變少了，所以專精的人越少，將會越有機會。易見地，也越來越少大學開設這門編譯器的課程，不過在一些公司，編譯器的技術將成為私囊秘寶，如何將代碼更加地優化快速，這就是相當令人感到為之一驚的地方。

DFA, NFA, Regular expression

在討論所有語法前，要明白正規表達式 ( Regular expression = RegExp ) 的運作，RegExp 運作上涵蓋的語法集合是最小的，對於一個 RegExp 來說，可以轉換成具有 n 個狀態的 NFA，而這台 NFA 可以轉換成 2ⁿ 狀態的 DFA。

NFA 和 DFA 最大的不同在於轉移狀態時，考慮的路徑情況，NFA 可以在不考慮輸入進行轉移，或者在相同情況下可以有很多轉移選擇。 DFA 則必須在一個輸入唯一一個轉移情況下運作。

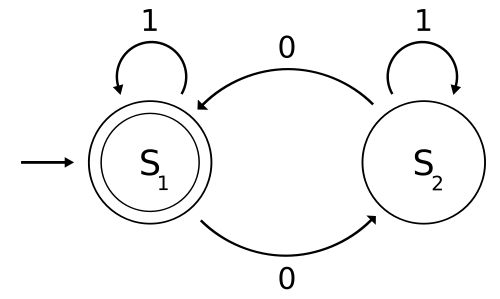
如上圖 DFA 所示，邊上的內容就是根據輸入的情況進行轉移。

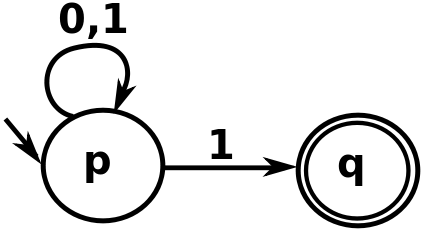
如上圖 NFA 所示，會發現狀態 p 對於輸入 1 有 2 種轉移可能 (p->p or p->q)。

最後可以得到一個 RegExp 一定會有一台 DFA 辨識它。而一台 DFA 也一定會有一個 RegExp，這句話的含意將可以在 計算理論 這門課中學到如何藉由類似 Floyd Algorithm 內點性質依序推出 DFA 對應的 RegExp。

CFG (Context-free grammar)

A context-free grammar is a formal system that describes a language by specifying how any legal string (i.e., sequence of tokens) can be derived from a start symbol. It consists of a set of productions, each of which states that a given symbol can be replaced by a given sequence of symbols.

另一個類似的語言是 Context-sensitive grammar，等價性質的兄弟是 Chomsky normal form。

• CFG G = (Vt, Vn, S, P)

  • Vt: 有限的 terminal 字符集
  • Vn: 有限的 nonterminal 字符集
  • S: 一開始出發的 start symbol
  • P: 轉換的規則 (production)

  • 來個例子

    LHS (left-hand side) -> RHS (right-hand side)
    
    <E>         -> <Prefix> ( <E> )
    <E>         -> V <Tail>
    <Prefix>    -> F
    <Prefix>    -> l
    <Tail>      -> + <E>
    <Tail>      -> l
    

    明顯地

    • Vt = {(, ), V, F, l, +}
    • Vn = {<E>, <Prefix>, <Tail>}
    • S = <E>
    • P 就是給定那六條規規則

• 名詞
  • Sentential form
    If S =>^* β, β then is said to be sentential form of the CFG
    簡單來說，所有從 start symbol 過程中替換出來的句子都稱為 sentential form。
  • Handle of a sentential form
    The handle of a sentential form is the left-most simple phrase.
    
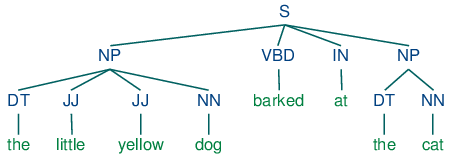
    簡單來說，就是將一個 nonterminal 根據 production 轉換成 RHS (right-hand side) 的一個步驟。

• 什麼是 CFG (上下文無關語法)？
  簡單來說，還真的是上下文無關，例如 S -> AB 可以見到 S 轉換時，不會因為前文或後文是什麼內容而影響，而在 Context-sensitive grammar (上下文敏感) 可以見到 aSb -> AB 會因為前面跟後面所受到的影響。

這裡使用大寫為 nontermainl，其他字符為 terminal。

First Set

• First(A)
  • The set of all the terminal symbols that can begin a sentential form derivable from A. A =>* aB

    First(A) = {
        a in Vt | A =>* aB, and
        Λ in Vt | A =>* Λ
    }
    

  • 簡單地說，從這個 nonterminal 開始，第一個不能被替換的 terminal 就會在 First set 中。
• 計算 First(A) 前，必須先建出這個 nonterminal 有沒有可能推出 Λ，即 A =>* Λ。
  這邊相當有意思，使用迭代更新，如果發現 B =>* Λ 和 C =>* Λ 則對於 Production A => BC 來說，可以得到 A =>* Λ 就這麼依序推出所有情況，時間複雜度應該在 O(n^2)。
• 計算 First(A) 時，掃描規則 LHS => RHS，找到 First(RHS) 並且 First(LHS).insert(First(RHS))，依樣使用迭代更新推出所有情況，時間複雜度應該在 O(n^2)。

Follow Set

• Follow(A)
  • A is any nonterminal
  • Follow(A) is the set of terminals that may follow A in some sentential form. S =>* ... Aabc ...follow set。

    Follow(A) = {
        a in Vt | S =>* ... Aa ..., and
        Λ in Vt | S =>* aA
    }
    

  • 請切記，一定要從 start symbol 開始替換的所有句子，而在這個 nonterminal 隨後可能跟著的 termainl 就會屬於它的。
• 計算 Follow(A) 前，請先把 First set 都算完，接著也是用迭代更新，掃描規則 A -> a B b
  對於

  if Λ not in First(b)
      Follow(B).insert(First(b))
  else
      Follow(B).insert(First(b) - Λ)
      Follow(B).insert(Follow(A))
  ``` 
  
  ## Predict Set ##
  
  * Given the productions
  * During a (leftmost) derivation, Deciding which production to match, Using lookahead symbols
  * 相較於 First set 和 Follow set，Predict Set 是根據 Production 產生的，也就是說一條 production 會有一個對應的 predict set，而 First set 和 Follow set 都是根據 nonterminal 產生一對一對應的集合，用來預測這一條規則的第一個 terminal 會有哪些。
  
  對於 production : `A -> X1 X2 ... Xm`

if Λ in First(X1 X2 … Xm)
Predict(A -> X1 X2 … Xm).insert(First(X1 X2 … Xm) - Λ);
Predict(A -> X1 X2 … Xm).insert(Follow(A));
else
Predict(A -> X1 X2 … Xm).insert(First(X1 X2 … Xm));

對於第一判斷情況在于 `... AE = ... X1 X2 ... Xm E`，明顯地可以從 `Follow(A)` 得到第一個字符為何。

## LL(1) Table ##
> 尚未撰寫

C++ code
=====

## 資料規格 ##

以下代碼實作 CFG 的 First Set, Follow Set, Predict Set 和 LL(1) Table。

用字符 `l` 代替 lambda

## 資料範例 ##

* 本課程簡易範例輸入

S->aSe
S->B
B->bBe
B->C
C->cCe
C->d

A->BaAb
A->cC
B->d
B->l
C->eA
C->l

A->aAd
A->B
B->bBd
B->C
C->cCd
C->l

E->TX
X->+E
X->#
T->(E)
T->intY
Y->*T
Y->#

E->P(E)
E->vT
P->f
P->l
T->+E
T->l

S->aSe
S->B
B->bBe
B->C
C->cCe
C->d

S->ABc
A->a
A->l
B->b
B->l

* 本課程簡易範例輸出

B:b,c,d
C:c,d
S:a,b,c,d
a:a
b:b
c:c
d:d
e:e
A:a,c,d
B:d,l
C:e,l
a:a
b:b
c:c
d:d
e:e
A:a,b,c,l
B:b,c,l
C:c,l
a:a
b:b
c:c
d:d

#:#
(:(
):)
:
+:+
E:(,i
T:(,i
X:#,+
Y:#,*
i:i
n:n
t:t
(:(
):)
+:+
E:(,f,v
P:f,l
T:+,l
f:f
v:v
B:b,c,d
C:c,d
S:a,b,c,d
a:a
b:b
c:c
d:d
e:e
A:a,l
B:b,l
S:a,b,c
a:a
b:b
c:c

- - - - -

* HTML 格式範例輸入

-> begin end
->
->
-> l
-> ID := ;
-> read ( ) ;
-> write ( ) ;
-> ID
-> , ID
-> l
->
-> ,
-> l
->
->
-> l
-> ( )
-> ID
-> INTLIT
-> +
-> -
-> $

begin ID := ID - INTLIT + ID ; end $

* HTML 格式範例輸出

+—————-+—– First set —–+
|$ | { $ }
|( | { ( }
|) | { ) }
|+ | { + }
|, | { , }
|- | { - }
|:= | { := }
|; | { ; }
| | { + - }
| | { ( ID INTLIT }
| | { , l }
| | { ( ID INTLIT }
| | { ID }
| | { , l }
| | { ( ID INTLIT }
| | { + - l }
| | { begin }
| | { ID read write }
|| { ID read write }
|| { ID l read write }
| | { begin }
|ID | { ID }
|INTLIT | { INTLIT }
|begin | { begin }
|end | { end }
|read | { read }
|write | { write }
+—————-+———————+

+—————-+—– Follow set —–+
| | { ( ID INTLIT }
| | { ) }
| | { ) }
| | { ) , ; }
| | { ) }
| | { ) }
| | { ) + , - ; }
| | { ) , ; }
| | { $ }
| | { ID end read write }
|| { end }
|| { end }
| | { l }
+—————-+———————+

+—————-+—– LL(1) table —–+
| | $| (| )| +| ,| -| :=| ;| ID|INTLIT| begin| end| read| write|
| | | | | 20| | 21| | | | | | | | |
| | | 11| | | | | | | 11| 11| | | | |
| | | | 13| | 12| | | | | | | | | |
| | | 14| | | | | | | 14| 14| | | | |
| | | | | | | | | | 8| | | | | |
| | | | 10| | 9| | | | | | | | | |
| | | 17| | | | | | | 18| 19| | | | |
| | | | 16| 15| 16| 15| | 16| | | | | | |
| | | | | | | | | | | | 1| | | |
| | | | | | | | | | 5| | | | 6| 7|
|| | | | | | | | | 2| | | | 2| 2|
|| | | | | | | | | 3| | | 4| 3| 3|
| | | | | | | | | | | | 22| | | |
+—————-+———————+

Process syntax accept

```

代碼

2014/6/1 修正 parsing 時的 lambda 問題。

#include <stdio.h> 
#include <vector>
#include <iostream>
#include <sstream>
#include <string>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include <ctype.h>
#include <assert.h>
using namespace std;

#define HTMLProduction

class Production {
    public:
        string 			LHS;
        vector<string> 	RHS;
        int 			label;
        
        Production(string L = "", vector<string> R = vector<string>()) {
            LHS = L;
            RHS = R;
        }
        
        void print() {
            printf("%s -> ", LHS.c_str());
            for(size_t i = 0; i < RHS.size(); i++)
                printf("%s", RHS[i].c_str());
        }
};
class Grammar {
    public:
        static const string 		lambda;
        string 						start_symbol;
        vector<Production> 			rules;
        map<string, set<string> > 	first_set;
        map<string, set<string> > 	follow_set;
        map<string, bool> 			derives_lambda;
        map<string, map<string, Production> >	lltable;
        
        map<string, bool> mark_lambda();
        void fill_first_set();
        void fill_follow_set();
        bool isNonterminal(string token);
        set<string> compute_first(vector<string> rhs);
        set<string> get_predict_set(Production p);
        void fill_lltable();
        void lldriver(queue<string> tokens);
};
const string Grammar::lambda("l");

set<string> Grammar::compute_first(vector<string> rhs) {
    set<string> result;
    size_t i;
    
    if(rhs.size() == 0 || rhs[0] == Grammar::lambda) {
        result.insert(Grammar::lambda);
    } else {
        result = first_set[rhs[0]];
        for(i = 1; i < rhs.size() && 
            first_set[rhs[i-1]].find(Grammar::lambda) != first_set[rhs[i-1]].end(); i++) {
            set<string> f = first_set[rhs[i]];
            f.erase(Grammar::lambda);
            result.insert(f.begin(), f.end());	
        }
        if(i == rhs.size() 
            && first_set[rhs[i-1]].find(Grammar::lambda) != first_set[rhs[i-1]].end()) {
            result.insert(Grammar::lambda);
        } else {
            result.erase(Grammar::lambda);
        }
    }
    
    return result;
} 
/*
 * please call get_predict_set() after fill_follow_set() and fill_first_set()
 */
set<string> Grammar::get_predict_set(Production p) {
    set<string> result;
    set<string> rfirst;
    
    rfirst = compute_first(p.RHS);
    if(rfirst.find(Grammar::lambda) != rfirst.end()) {
        rfirst.erase(Grammar::lambda);
        result.insert(rfirst.begin(), rfirst.end());
        rfirst = follow_set[p.LHS];
        result.insert(rfirst.begin(), rfirst.end());
    } else {
        result.insert(rfirst.begin(), rfirst.end());
    }
    
    return result;
}
/*
 * 
 */
void Grammar::fill_lltable() {
    string		A; // nonterminal
    Production 	p;
    
    for(size_t i = 0; i < rules.size(); i++) {
        p = rules[i];
        A = p.LHS;
        set<string> predict_set = get_predict_set(p);
        
        for(set<string>::iterator it = predict_set.begin();
            it != predict_set.end(); it++) {
            assert(lltable[A].find(*it) == lltable[A].end());
            lltable[A][*it] = p;
        }
    }
    
}
bool Grammar::isNonterminal(string token) {

#ifdef HTMLProduction
    if(token == Grammar::lambda)
        return false;
    if(token[0] == '<' && token[token.length() - 1] == '>')
        return true;
    return false;
#else
    if(token == Grammar::lambda)
        return false;
    for(size_t i = 0; i < token.length(); i++) {
        if(isupper(token[i]))
            return true;
    }
    return false;
#endif
}
map<string, bool> Grammar::mark_lambda() {
    bool 				rhs_derives_lambda;
    bool 				changes;
    Production 			p;
    
    derives_lambda.clear();
    
    /* initially, nothing is marked. */
    for(size_t i = 0; i < rules.size(); i++) {
        derives_lambda[rules[i].LHS] = false;
    }
    do {
        changes = false;
        for(size_t i = 0; i < rules.size(); i++) {
            p = rules[i];
            if(!derives_lambda[p.LHS]) {
                if(p.RHS.size() == 0 || p.RHS[0] == Grammar::lambda) {
                    changes = derives_lambda[p.LHS] = true;
                    continue;
                }
                /* does each part of RHS derive lambda ? */
                rhs_derives_lambda = derives_lambda[string(p.RHS[0])];
                for(size_t j = 1; j < p.RHS.size(); j++) {
                    rhs_derives_lambda &= derives_lambda[p.RHS[j]];
                }
                if(rhs_derives_lambda) {
                    changes = true;
                    derives_lambda[p.LHS] = true;
                }
            }
        }
    } while(changes);
    return derives_lambda;
}
void Grammar::fill_first_set() {
    
    string 		A; // nonterminal
    string 		a; // terminal
    Production 	p;
    bool 		changes;
        
    mark_lambda();
    first_set.clear();
    
    for(size_t i = 0; i < rules.size(); i++) {
        A = rules[i].LHS;
        if(derives_lambda[A])
            first_set[A].insert(Grammar::lambda);
    }
    
    for(size_t i = 0; i < rules.size(); i++) {
        for(size_t j = 0; j < rules[i].RHS.size(); j++) {
            a = rules[i].RHS[j];
            if(!isNonterminal(a)) {
                if(a != Grammar::lambda)
                    first_set[a].insert(a);
                if(j == 0) { // A -> aXX
                    first_set[rules[i].LHS].insert(a);
                }
            }
        }
    }
    
    do {
        changes = false;
        for(size_t i = 0; i < rules.size(); i++) {
            p = rules[i];
            set<string> rfirst = compute_first(p.RHS);
            size_t oldsize = first_set[p.LHS].size();
            first_set[p.LHS].insert(rfirst.begin(), rfirst.end());
            size_t newsize = first_set[p.LHS].size();
            if(oldsize != newsize)
                changes = true;
        }
    } while(changes);
} 

void Grammar::fill_follow_set() {
    string 	A, B; // nonterminal
    Production 	p;
    bool 	changes;
    
    for(size_t i = 0; i < rules.size(); i++) {
        A = rules[i].LHS;
        follow_set[A].clear();
    }
    
    follow_set[start_symbol].insert(Grammar::lambda);
        
    do {
        changes = false;
        for(size_t i = 0; i < rules.size(); i++) {
            /* A -> a B b
			 * I.e. for each production and each occurrence
			 * of a nonterminal in its right-hand side. 
			 */
            p = rules[i];
            A = p.LHS;
            for(size_t j = 0; j < p.RHS.size(); j++) {
                B = p.RHS[j];
                if(isNonterminal(B)) {
                    vector<string> beta(p.RHS.begin() + j + 1, p.RHS.end());
                    set<string> rfirst = compute_first(beta);
                    size_t oldsize = follow_set[B].size();
                    
                    if(rfirst.find(Grammar::lambda) == rfirst.end()) {
                        follow_set[B].insert(rfirst.begin(), rfirst.end());	
                    } else {
                        rfirst.erase(Grammar::lambda);
                        follow_set[B].insert(rfirst.begin(), rfirst.end());	
                        rfirst = follow_set[A];
                        follow_set[B].insert(rfirst.begin(), rfirst.end());
                    }
                    size_t newsize = follow_set[B].size();			
                    if(oldsize != newsize)
                        changes = true;
                }
            }
        }
    } while(changes);
}

void Grammar::lldriver(queue<string> tokens) {
    stack<string> 	stk;
    string 			X;
    string			a;
    Production		p;
    /* Push the Start Symbol onto an empty stack */
    stk.push(start_symbol);
    
    while(!stk.empty() && !tokens.empty()) {
        X = stk.top();
        a = tokens.front();
        // cout << X << " " << a << endl;
        if(isNonterminal(X) && lltable[X].find(a) != lltable[X].end()) {
            p = lltable[X][a];
            stk.pop();
            for(int i = p.RHS.size() - 1; i >= 0; i--) {
                if(p.RHS[i] == Grammar::lambda)
                    continue;
                stk.push(p.RHS[i]);
            }
        } else if(X == a) {
            stk.pop();
            tokens.pop();
        } else if(lltable[X].find(Grammar::lambda) != lltable[X].end()) {
            stk.pop();
        } else {
            /* Process syntax error. */
            puts("Bad!");
            return;
        }
    }
    while(!stk.empty()) {
        X = stk.top();
        if(lltable[X].find(Grammar::lambda) != lltable[X].end())
            stk.pop();
        else
            break;
    }
    if(tokens.size() == 0 && stk.size() == 0)
        puts("Good");
    else
        puts("Bad!");
    return;
}

queue<string> getTokens(char s[]) {
    stringstream 	sin(s);
    queue<string> 	tokens;
    string			token;
    while(sin >> token)
        tokens.push(token);
    return tokens;
}

void parsingProduction(string r, Grammar &g) {
#ifdef HTMLProduction
    static int 		production_label = 0;
    stringstream 	sin(r);
    string 			lhs, foo;
    vector<string> 	tokens;
    sin >> lhs >> foo;
    while(sin >> foo)
        tokens.push_back(foo);
    Production p(lhs, tokens);
    p.label = ++production_label;
    g.rules.push_back(p);
#else
    string div("->");
    size_t found = r.find(div);
    if(found != std::string::npos) {
        string rhs = r.substr(found + div.length());
        vector<string> tokens;
        for(size_t i = 0; i < rhs.size(); i++)
            tokens.push_back(rhs.substr(i, 1));
        Production p(r.substr(0, found), tokens);
        g.rules.push_back(p);
    }
#endif
} 

int main() {
    
    //freopen("input.txt", "r+t", stdin);
    //freopen("output.txt", "w+t", stdout); 
    
    char in[1024];
    while(gets(in)) {
        Grammar g;
        parsingProduction(in, g);
        while(gets(in) && in[0] != '\0') {
            parsingProduction(in, g);
        }
        
#ifdef HTMLProduction
        g.start_symbol = "<system_goal>";
#else
        g.start_symbol = "S";
#endif
        
        g.fill_first_set();
        g.fill_follow_set();
        g.fill_lltable();
        
        puts("+----------------+----- First set -----+");
        for(map<string, set<string> >::iterator it = g.first_set.begin();
            it != g.first_set.end(); it++) {
            printf("|%-16s| {", it->first.c_str());
            for(set<string>::iterator jt = it->second.begin();
                jt != it->second.end(); jt++) {
                cout << " " << *jt;
            }
            puts(" }");
        }
        puts("+----------------+---------------------+\n");
        puts("+----------------+----- Follow set -----+");
        for(map<string, set<string> >::iterator it = g.follow_set.begin();
            it != g.follow_set.end(); it++) {
            printf("|%-16s| {", it->first.c_str());
            for(set<string>::iterator jt = it->second.begin();
                jt != it->second.end(); jt++) {
                cout << " " << *jt;
            }
            puts(" }");
        }
        puts("+----------------+---------------------+\n");
        puts("+----------------+----- LL(1) table -----+");
        printf("|%-16s|", "");			
        for(map<string, set<string> >::iterator jt = g.first_set.begin();
                jt != g.first_set.end(); jt++) {
            string A = jt->first;
            if(g.isNonterminal(A))
                continue;
            printf("%6s|", A.c_str());
        }
        puts("");
        for(map<string, map<string, Production> >::iterator it = g.lltable.begin();
            it != g.lltable.end(); it++) {
            printf("|%-16s|", it->first.c_str());
            for(map<string, set<string> >::iterator jt = g.first_set.begin();
                jt != g.first_set.end(); jt++) {
                string A = jt->first;
                if(g.isNonterminal(A))
                    continue;
                if(it->second.find(A) == it->second.end()) 
                    printf("%6s|", "");
                else
                    printf("%6d|", it->second[A].label);
            }
            puts("");
        }
        puts("+----------------+---------------------+\n");
#ifdef HTMLProduction
        gets(in);
        g.lldriver(getTokens(in));
#endif
    }
    return 0;
}

備註

要學會更多，請修 計算理論 這門課程。

Read More +