2014-06-24

UVa 427 - FlatLand Piano Movers

1. Problem
2. Input
3. Output
4. Sample Input
5. Sample Output
6. Solution

Problem

FlatLand Piano Movers, as part of their Total Quality Management project, has decided to focus on the job estimation process. Part of this process involves walking the proposed paths that are to be used to move a piano to see if it will fit through corridors and around corners. Now this is harder than it might seem, since FlatLand is a 2-dimensional world.

FlatLand pianos are rectangles of various sizes. FlatLand building codes require all turns in corridors to be right angle turns and prohibit T intersections. All dimensions are in furlongs. You can assume that each portion of a corridor is long enough so that other corners or doors into rooms don’t have any effect on getting around a turn. You can also assume that the piano is narrower than the width of any corridor. Note that the piano actually has to turn in the corner, since it can only be pushed or pulled on one of its shorter sides (there are no square pianos).

Your team’s job is to write a program for a palmtop computer that will determine if a given piano will fit around a corner in a corridor.

Input

The input consists of a series of lines up to 80 columns in width followed by the end-of-file. Each line consists of a series of number pairs. The numbers of a pair are separated by a comma and the pairs are separated by at least one space. The first pair is the size of a piano, and the remaining pairs are the widths of corridors on each side of the turns. Consider the example:

1	600,200 300,500 837,500 350,350

This is a 600 by 200 piano. The first turn is from a 300 furlong wide corridor through a right angle turn into a 500 furlong wide corridor. The next turn is from an 837 furlong wide corridor into one 500 furlongs wide. The last turn is from a 350 furlong wide corridor into another 350 furlong wide corridor.

Output

For each piano, your program is to produce a yes-or-no answer for each turn. If the piano will fit around the turn, print Y''; if not, printN’’. The results for each piano should be printed on a separate line.

Sample Input

1 2	600,200 300,500 837,500 350,350 137,1200 600,500 600,400

Sample Output

1
2

YYN
YN

Solution

題目描述：

一台鋼琴長寬 W, H，接著要經過一個 T 字路口，進去之後向右轉，一開始進去的寬度為 X，右轉之後的寬度為 Y，問能不能順利轉彎。

每組輸入給定一台鋼琴長寬，接著給定多組路口寬組合。

題目解法：

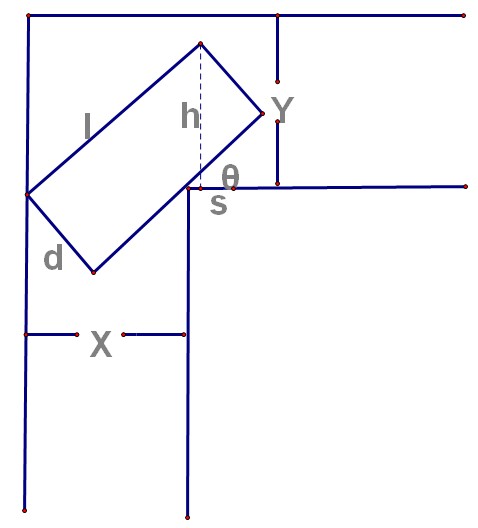
汽车拐弯问题，给定 X, Y, l, d 判断是否能够拐弯。首先当 X 或者 Y 小于 d，那么一定不能。
其次我们发现随着角度 θ 的增大，最大高度 h 先增长后减小，即为凸性函数，可以用三分法来求解。

这里的 Calc 函数需要比较繁琐的推倒公式：
s = l cos(θ) + w sin(θ) - x;
h = s tan(θ) + w cos(θ);
其中 s 为汽车最右边的点离拐角的水平距离, h 为里拐点最高的距离, θ 范围从 0 到 90。

轉貼備份www.cnblogs.com/newpanderking/archive/2011/08/25/2153777.html

看著大神給的三分搜索的式子，用簡單的凸性勾勒出來。

#include <stdio.h> 
#include <math.h>
#include <string.h>
#include <iostream>
#include <sstream>
#include <algorithm>
using namespace std;
// http://www.cnblogs.com/newpanderking/archive/2011/08/25/2153777.html
const double pi = acos(-1);
#define eps 1e-6 
double ternary_search(double H, double W, double X, double Y) {
    double l = 0, r = pi /2, mid, midmid;
    double s1, h1, s2, h2;
    while(fabs(l - r) > eps) {
        mid = (l + r) /2;
        midmid = (mid + r) /2;
        s1 = H * cos(mid) + W * sin(mid) - X;
        h1 = s1 * tan(mid) + W * cos(mid);
        s2 = H * cos(midmid) + W * sin(midmid) - X;
        h2 = s2 * tan(midmid) + W * cos(midmid);
        if(h1 < h2)
            l = mid;
        else
            r = mid;
    }
    return h1;
}
int main() {
    char line[1024];
    while(gets(line)) {
        stringstream sin(line);
        string token;
        sin >> token;
        double H, W, X, Y;
        sscanf(token.c_str(), "%lf,%lf", &H, &W);
        if(H < W)
            swap(H, W);
        while(sin >> token) {
            sscanf(token.c_str(), "%lf,%lf", &X, &Y);
            double h = ternary_search(H, W, X, Y);
            printf("%c", h <= Y ? 'Y' : 'N');
        }
        puts("");
    }
    return 0;
}

Morris' Blog